Question

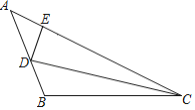
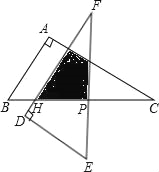
【题目】如图△ABC中，∠A=90°，∠C=30°，BC=12cm，把△ABC绕着它的斜边中点P逆时针旋转90°至△DEF的位置，DF交BC于点H．

（1）PH=_____cm．

（2）△ABC与△DEF重叠部分的面积为_____cm2．

Answer 1

【答案】

【解析】

如图，由点P为斜边BC的中点得到PC=BC=6，再根据旋转的性质得PF=PC=6，∠FPC=90°，∠F=∠C=30°，根据含30度的直角三角形三边的关系，在Rt△PFH中计算出PH=PF=2；在Rt△CPM中计算出PM=PC=2，且∠PMC=60°，则∠FMN=∠PMC=60°，于是有∠FNM=90°，FM=PF-PM=6-2，则在Rt△FMN中可计算出MN=FM=3-，FN=MN=3-3，然后根据三角形面积公式和利用△ABC与△DEF重叠部分的面积=S△FPH-S△FMN进行计算即可．

解：如图，

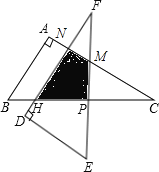
∵点P为斜边BC的中点，
∴PB=PC=BC=6，
∵△ABC绕着它的斜边中点P逆时针旋转90°至△DEF的位置，
∴PF=PC=6，∠FPC=90°，∠F=∠C=30°，
在Rt△PFH中，∵∠F=30°，

∴PH=PF=2，

在Rt△CPM中，∵∠C=30°，

∴PM=PC=2，∠PMC=60°，

∴∠FMN=∠PMC=60°，
∴∠FNM=90°，
∴FM=PF-PM=6-2，

在Rt△FMN中，∵∠F=30°，

∴MN=FM=3-，

∴FN=MN=3-3，

∴△ABC与△DEF重叠部分的面积=S△FPH-S△FMN

= ，

=9（cm2）．
故答案为： ； 9．