题目内容
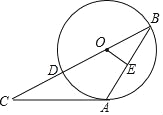
【题目】如图,BD是⊙O的直径,BA是⊙O的弦,过点A的切线交BD延长线于点C,OE⊥AB于E,且AB=AC,若CD=2![]() ,则OE的长为_____.
,则OE的长为_____.
【答案】![]()
【解析】
连接OA,所以∠OAC=90°,因为AB=AC,所以∠B=∠C,根据圆周角定理可知∠AOD=2∠B=2∠C,故可求出∠B和∠C的度数,在Rt△OAC中,求出OA的值,再在Rt△OAE中,求出OE的值,得到答案.
连接OA,由题意可知∠OAC=90°,∵AB=AC,∴∠B=∠C,,根据圆周角定理可知∠AOD=2∠B=2∠C,∵∠OAC=90°∴∠C+∠AOD=90°,∴∠C+2∠C=90°,故∠C=30°=∠B,∴在Rt△OAC中,sin∠C=![]() =
=![]() ,∴OC=2OA,∵OA=OD,∴OD+CD=2OA,∴CD=OA=2
,∴OC=2OA,∵OA=OD,∴OD+CD=2OA,∴CD=OA=2![]() ,∵OB=OA,∴∠OAE=∠B=30°,∴在Rt△OAE中,sin∠OAE=
,∵OB=OA,∴∠OAE=∠B=30°,∴在Rt△OAE中,sin∠OAE=![]() =
=![]() ,∴OA=2OE,∴OE=
,∴OA=2OE,∴OE=![]() OA=
OA=![]() ,故答案为
,故答案为![]() .
.

练习册系列答案
相关题目