��Ŀ����
����Ŀ����֪����ʽ2x3y��xy+16�Ĵ���Ϊa��������Ϊb��a��b�ֱ��Ӧ�������ϵ�A��B���㣮
��1��a= ��b= �����������ϻ���A��B���㣻
��2������P�ӵ�A��������ÿ��3����λ���ȵ�λ���ٶ���x���������˶������˶�ʱ��Ϊ����ʱ����P����A�ľ����ǵ�P����B�ľ����2����
��3�������ϻ���һ��C������Ϊ30������P��Qͬʱ�ӵ�A�͵�B�������ֱ���ÿ��3����λ���Ⱥ�ÿ��1����λ���ȵ��ٶ���C���˶���P����C�����������ͬ�����ٶȷ��أ��˶����յ�A�����P�͵�Q�˶�������ʱ��P��Q����֮��ľ���Ϊ4���������ʱ��Q�����꣮
���𰸡���1��4��16����2��![]() ��8�룻��3����P�͵�Q�˶���4��8��9��11��ʱ��P��Q����֮��ľ���Ϊ4��
��8�룻��3����P�͵�Q�˶���4��8��9��11��ʱ��P��Q����֮��ľ���Ϊ4��
�������������������1�����ݶ���ʽ�Ĵ�������������Ķ���Ϳ��Եó����ۣ��Ϳ������A��B����ʾ�����������������ϱ�ʾ���ɣ�
��2�����˶�ʱ��Ϊts�������⣺3t=2��16��4��3t����3t=2��4+3t��16�����ⷽ�̼��ɵ���
��3�����˶�ʱ��Ϊts�������⣺12+t��3t=4��3t����12+t��=4��12+t+4+3t=52��12+t+3t��4=52���ⷽ�̼��ɵ�.
�����������1���߶���ʽ2x3y��xy+16�Ĵ���Ϊa��������Ϊ b��
��a=4��b=16��
�ʴ�Ϊ4��16��
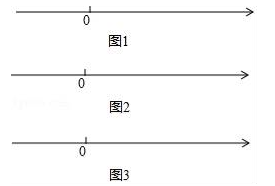
��A��B��λ����ͼ��ʾ��
![]()
��2�����˶�ʱ��Ϊts��
�����⣺3t=2��16��4��3t����3t=2��4+3t��16����
���t=![]() ��8��
��8��
���˶�ʱ��Ϊ![]() ��8��ʱ���� P����A�ľ����ǵ�P����B�ľ����2����
��8��ʱ���� P����A�ľ����ǵ�P����B�ľ����2����
��3�����˶�ʱ��Ϊts��
�����⣺12+t��3t=4��3t����12+t��=4��12+t+4+3t=52��12+t+3t��4=52��
���t=4��8��9��11��
���P�͵�Q�˶�ʱ��Ϊ4��8��9��11��ʱ��P��Q����֮��ľ���Ϊ4��

����Ŀ��ij�߲˾�Ӫ�����߲������г������߲˽������ۣ������߲������۸������ۼ۸������
�߲�Ʒ�� | ������ | �ཷ | ������ | ���� |
�����ۣ�Ԫ/�K�� | 3.6 | 5.4 | 8 | 4.8 |
���ۼۣ�Ԫ/�K�� | 5.4 | 8.4 | 14 | 7.6 |
�����������⣺
��1����һ�죬�þ�Ӫ�������������������������߲˹�300�K����ȥ��1520ԪǮ���������߲˵���ȫ������һ���˶���ԪǮ��
��2���ڶ��죬�þ�Ӫ����1520Ԫ��Ȼ��������������������Ҫ�뵱��ȫ���������Ǯ��������1050Ԫ����þ�Ӫ��������������������٩K��