题目内容
【题目】如图,在四边形ABCD中,对角线AC与BD相交于点E,若AC平分∠DAB,且AB=AC,AC=AD,有如下四个结论:①AC⊥BD;②BC=DE;③∠DBC=∠DAC;④△ABC是正三角形.请写出正确结论的序号(把你认为正确结论的序号都填上)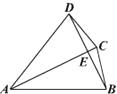
【答案】①
【解析】∵AB=AC,AC=AD,∴AB=AD∵AC平分∠DAB∴AC垂直平分BD,①正确;∴DC=CB,易知DC>DE,∴BC>DE,②错;D、C、B可看作是以点A为圆心的圆上,
∠DBC与∠DAC是圆心角与圆周角的关系,③错误;当△ABC是正三角形时,∠CAB=60°
那么∠DAB=120°,如图所示是不可能的,所以错误.故①的结论正确.
【考点精析】利用线段垂直平分线的性质对题目进行判断即可得到答案,需要熟知垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等.

练习册系列答案
相关题目