题目内容
【题目】在
ABCD中，∠ADC的平分线交直线BC于点E、交AB的延长线于点F，连接AC.
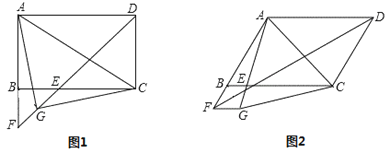
（1）如图1，若∠ADC=90°，G是EF的中点，连接AG、CG.
①求证：BE=BF；
②请判断△AGC的形状，并说明理由.
（2）如图2，若∠ADC=60°，将线段FB绕点F顺时针旋转60°至FG，连接AG、CG，判断△AGC的形状.（直接写出结论不必证明）
【答案】（1）①证明见解析；②△AGC是等腰直角三角形．证明见解析；（2）△AGC是等边三角形.
【解析】试题分析：（1）①先判定四边形ABCD是矩形，再根据矩形的性质可得∠ABC=90°，AB∥DC，AD∥BC，然后根据平行线的性质求出∠F=∠FDC，∠BEF=∠ADF，再根据DF是∠ADC的平分线，利用角平分线的定义得到∠ADF=∠FDC，从而得到∠F=∠BEF，然后根据等角对等边的性质即可证明；
②连接BG，根据等腰直角三角形的性质可得∠F=∠BEF=45°，再根据等腰三角形三线合一的性质求出BG=FG，∠F=∠CBG=45°，然后利用“边角边”证明△AFG和△CBG全等，根据全等三角形对应边相等可得AG=CG，再求出∠GAC+∠ACG=90°，然后求出∠AGC=90°，然后根据等腰直角三角形的定义判断即可；
（2）连接BG，根据旋转的性质可得△BFG是等边三角形，再根据角平分线的定义以及平行线的性质求出AF=AD，平行四边形的对角相等求出∠ABC=∠ADC=60°，然后求出∠CBG=60°，从而得到∠AFG=∠CBG，然后利用“边角边”证明△AFG和△CBG全等，根据全等三角形对应边相等可得AG=CG，全等三角形对应角相等可得∠FAG=∠BCG，然后求出∠GAC+∠ACG=120°，再求出∠AGC=60°，然后根据等边三角形的判定方法判定即可．
试题解析：（1）证明：①∵四边形ABCD是平行四边形，∠ADC=90°，
∴四边形ABCD是矩形，∴∠ABC=90°，AB∥DC，AD∥BC，
∴∠F=∠FDC，∠BEF=∠ADF，
∵DF是∠ADC的平分线，∴∠ADF=∠FDC，∴∠F=∠BEF，
∴BF=BE；
②△AGC是等腰直角三角形．
理由如下：连接BG，
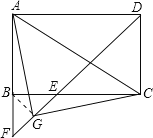
由①知，BF=BE，∠FBC=90°，∴∠F=∠BEF=45°，
∵G是EF的中点，∴BG=FG，∠F=∠CBG=45°，
∵∠FAD=90°，∴AF=AD，又∵AD=BC，∴AF=BC，
在△AFG和△CBG中，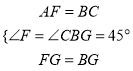 
∴△AFG≌△CBG，
∴AG=CG，∠FAG=∠BCG，
又∵∠FAG+∠GAC+∠ACB=90°，∴∠BCG+∠GAC+∠ACB=90°，
即∠GAC+∠ACG=90°，∴∠AGC=90°，∴△AGC是等腰直角三角形；
(2)△AGC是等边三角形.
证明：连接BG，∵FB绕点F顺时针旋转60°至FG，
∴△BFG是等边三角形，
∴FG=BG，∠FBG=60°，
又∵四边形ABCD是平行四边形，∠ADC=60°，
∴∠ABC=∠ADC=60°
∴∠CBG=180°-∠FBG-∠ABC=180°-60°-60°=60°，
∴∠AFG=∠CBG，
∵DF是∠ADC的平分线，
∴∠ADF=∠FDC，
∵AB∥DC，
∴∠AFD=∠FDC，
∴∠AFD=∠ADF，
∴AF=AD，
在△AFG和△CBG中，
，
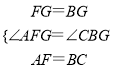∴△AFG≌△CBG（SAS），
∴AG=CG，∠FAG=∠BCG，
在△ABC中，∠GAC+∠ACG=∠ACB+∠BCG+∠GAC=∠ACB+∠BAG+∠GAC=∠ACB+∠BAC=180°-60°=120°，
∴∠AGC=180°-（∠GAC+∠ACG）=180°-120°=60°，
∴△AGC是等边三角形．
