题目内容
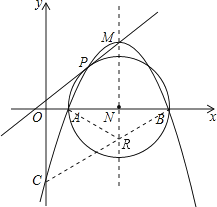
【题目】如图,已知抛物线y=![]() (x2﹣7x+6)的顶点坐标为M,与x轴相交于A,B两点(点B在点A的右侧),与y轴相交于点C.
(x2﹣7x+6)的顶点坐标为M,与x轴相交于A,B两点(点B在点A的右侧),与y轴相交于点C.
(1)用配方法将抛物线的解析式化为顶点式:y=a(x﹣h)2+k(a≠0),并指出顶点M的坐标;
(2)在抛物线的对称轴上找点R,使得CR+AR的值最小,并求出其最小值和点R的坐标;
(3)以AB为直径作⊙N交抛物线于点P(点P在对称轴的左侧),求证:直线MP是⊙N的切线.
【答案】
(1)
【解答】解:∵y=![]() (x2﹣7x+6)=
(x2﹣7x+6)=![]() (x2﹣7x)﹣3=
(x2﹣7x)﹣3=![]() (x﹣
(x﹣![]() )2+
)2+![]() ,
,
∴抛物线的解析式化为顶点式为:y=![]() (x﹣
(x﹣![]() )2+
)2+![]() ,
,
顶点M的坐标是(![]() ,
,![]() );
);
(2)
解:∵y=![]() (x2﹣7x+6),
(x2﹣7x+6),
∴当y=0时,![]() (x2﹣7x+6)=0,
(x2﹣7x+6)=0,
解得x=1或6,
∴A(1,0),B(6,0),
∵x=0时,y=﹣3,
∴C(0,﹣3).
连接BC,则BC与对称轴x=![]() 的交点为R,连接AR,
的交点为R,连接AR,
则CR+AR=CR+BR=BC,根据两点之间线段最短可知此时CR+AR的值最小,
最小值为BC=![]() =
=![]() .
.
设直线BC的解析式为y=kx+b,
∵B(6,0),C(0,﹣3),
∴![]() ,
,
解得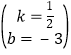 ,
,
∴直线BC的解析式为:y=![]() x﹣3,
x﹣3,
令x=![]() ,得y=
,得y=![]() ×
×![]() ﹣3=
﹣3=![]() ,
,
∴R点坐标为(![]() ,
,![]() );
);
(3)
证明:设点P坐标为(x,![]() x2+
x2+![]() x﹣3).
x﹣3).
∵A(1,0),B(6,0),
∴N(![]() ,0),
,0),
∴以AB为直径的⊙N的半径为![]() AB=
AB=![]() ,
,
∴NP=![]() ,
,
即(x﹣![]() )2+(
)2+(![]() x2+
x2+![]() x﹣3)2=(
x﹣3)2=(![]() )2,
)2,
化简整理得,x4﹣14x3+65x2﹣112x+60=0,
(x﹣1)(x﹣2)(x﹣5)(x﹣6)=0,
解得x1=1(与A重合,舍去),x2=2,x3=5(在对称轴的右侧,舍去),x4=6(与B重合,舍去),
∴点P坐标为(2,2).
∵M(![]() ,
,![]() ),N(
),N(![]() ,0),
,0),
∴PM2=(2﹣![]() )2+(2﹣
)2+(2﹣![]() )2=
)2=![]() ,
,
PN2=(2﹣![]() )2+22=
)2+22=![]() =
=![]() ,
,
MN2=(![]() )2=
)2=![]() ,
,
∴PM2+PN2=MN2,
∴∠MPN=90°,
∵点P在⊙N上,
∴直线MP是⊙N的切线.
【解析】(1)利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,即可把一般式转化为顶点式,然后根据二次函数的性质求出抛物线的顶点坐标;
(2)连接BC,则BC与对称轴的交点为R,此时CR+AR的值最小;先求出点A、B、C的坐标,再利用待定系数法求出直线BC的解析式,进而求出其最小值和点R的坐标;
(3)设点P坐标为(x,﹣![]() x2+
x2+![]() x﹣3).根据NP=
x﹣3).根据NP=![]() AB=
AB=![]() 列出方程(x﹣
列出方程(x﹣![]() )2+(﹣
)2+(﹣![]() x2+
x2+![]() x﹣3)2=(
x﹣3)2=(![]() )2 , 解方程得到点P坐标,再计算得出PM2+PN2=MN2 , 根据勾股定理的逆定理得出∠MPN=90°,然后利用切线的判定定理即可证明直线MP是⊙N的切线.
)2 , 解方程得到点P坐标,再计算得出PM2+PN2=MN2 , 根据勾股定理的逆定理得出∠MPN=90°,然后利用切线的判定定理即可证明直线MP是⊙N的切线.

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案