题目内容
【题目】已知抛物线y=ax2+bx+3的对称轴是直线x=1．
（1）求证：2a+b=0
（2）若关于x的方程ax2+bx﹣8=0的一个根为4，求方程的另一个根．
【答案】
（1）
证明：∵对称轴是直线x=1=﹣
，
∴2a+b=0；
（2）
解：∵ax2+bx﹣8=0的一个根为4，
∴16a+4b﹣8=0，
∵2a+b=0，
∴b=﹣2a，
∴16a﹣8a﹣8=0，
解得：a=1，则b=﹣2，
∴ax2+bx﹣8=0为：x2﹣2x﹣8=0，
则（x﹣4）（x+2）=0，
解得：x1=4，x2=﹣2，
故方程的另一个根为：﹣2．
【解析】（1）直接利用对称轴公式代入求出即可；
（2）根据（1）中所求，再将x=4代入方程求出a，b的值，进而解方程得出即可．
此题考查了二次函数的应用，涉及知识点有二次函数的对称轴性质，二次函数与系数关系.
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
【题目】某市团委举办“我的中国梦”为主题的知识竞赛，甲、乙两所学校参赛人数相等，比赛结束后，发现学生成绩分别为70分，80分，90分，100分，并根据统计数据绘制了如下不完整的统计图表：
乙校成绩统计表
分数（分） | 人数（人） |
70 | 7 |
80 | |
90 | 1 |
100 | 8 |
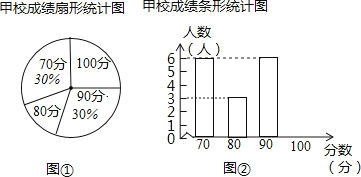
（1）在图①中，“80分”所在扇形的圆心角度数为 ；
（2）请你将图②补充完整；
（3）求乙校成绩的平均分；
（4）经计算知S甲2=135，S乙2=175，请你根据这两个数据，对甲、乙两校成绩作出合理评价．
