题目内容
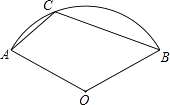
【题目】根据道路管理规定,在贺州某段笔直公路上行驶的车辆,限速40千米/时,已知交警测速点M到该公路A点的距离为![]() 米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.
米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.
(1)求测速点M到该公路的距离;
(2)通过计算判断此车是否超速.(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)
【答案】
(1)
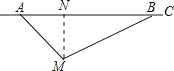
【解答】解:过M作MN⊥AB,
在Rt△AMN中,AM=![]() ,∠MAN=45°,
,∠MAN=45°,
∴sin∠MAN=![]() ,即
,即![]() ,
,
解得:MN=10,
则测速点M到该公路的距离为10米;
(2)
由1知:AN=MN=10米,
在Rt△MNB中,∠MBN=30°,
由tan∠MBN=![]() ,得:
,得:![]() ,
,
解得:BN=![]() (米),
(米),
∴AB=AN+NB=10+![]() ≈27.3(米),
≈27.3(米),
∴汽车从A到B的平均速度为27.3÷3=9.1(米/秒),
∵9.1米/秒=32.76千米/时<40千米/时,
∴此车没有超速.
【解析】

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
【题目】某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如下不完整的统计图表:
乙校成绩统计表
分数(分) | 人数(人) |
70 | 7 |
80 | |
90 | 1 |
100 | 8 |
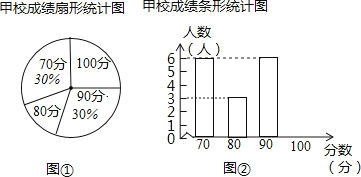
(1)在图①中,“80分”所在扇形的圆心角度数为 ;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;
(4)经计算知S甲2=135,S乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.