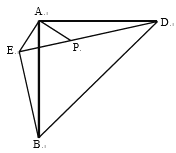
题目内容
【题目】如图，在平面直角坐标系中，点
、
分别在笫一、二象限，
轴于点
，连接
、
、
，且
（1）如图1，若
，
，
，探究
、
之间的数量关系，并证明你的结论
（2）如图2，若
，
，探究线段
、之间的数量关系，并证明你的结论．
【答案】（1）
，证明见解析；（2）
，证明见解析
【解析】
（1）过点
做
轴于
，利用AAS定理证明
，从而得到
，
，然后利用等腰直角三角形的判定与性质得到
，即
，从而求出a，b的关系；
（2）在
轴上取一点，使得
，根据含60°角的等腰三角形是等边三角形判定
，
是等边三角形，然后利用SAS定理证明
，从而得到
，
，然后利用含30°的直角三角形的性质求证．
解：（1）如图1，过点做轴于，
则
∴
∴
∵
，
∴（AAS）
∴ ，
∵
，
∴
∴
∴
∴．
（2）如图2，在轴上取一点，使得
∵
∴
∴是等边三角形
∴
∵
∴是等边三角形
∴
∴
∴（SAS）
∴，
∴
∵
∴
∴
∴．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
【题目】郑州市自2019年12月1日起推行垃圾分类，广大市民对垃圾桶的需求剧增．为满足市场需求，某超市花了7900元购进大小不同的两种垃圾桶共800个，其中，大桶和小桶的进价及售价如表所示．
大桶 | 小桶 | |
进价（元/个） | 18 | 5 |
售价（元/个） | 20 | 8 |
（1）该超市购进大桶和小桶各多少个？
（2）当小桶售出了300个后，商家决定将剩下的小桶的售价降低1元销售，并把其中一定数量的小桶作为赠品，在顾客购买大桶时，买一赠一（买一个大桶送一个小桶），送完即止．
请问：超市要使这批垃圾桶售完后获得的利润为1550元，那么小桶作为赠品送出多少个？
