题目内容
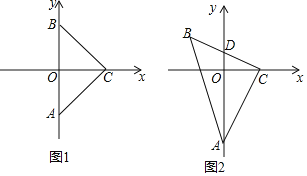
【题目】如图,在△![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒
以每秒![]() 的速度向点
的速度向点![]() 运动,同时点
运动,同时点![]() 从
从![]() 点出发,沿
点出发,沿![]() 以
以![]() 的速度向点
的速度向点![]() 运动,设运动时间为
运动,设运动时间为![]() 秒
秒
(1)当![]() 为何值时,
为何值时,![]() .
.
(2)当![]() 为何值时,
为何值时,![]() ∥
∥![]() .
.
(3)△![]() 能否与△
能否与△![]() 相似?若能,求出
相似?若能,求出![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.

【答案】(1)![]() 秒;(2)
秒;(2)![]() 秒;(3)能,
秒;(3)能,![]() 秒或5秒
秒或5秒
【解析】
(1)分别用x表示出线段BP和CQ的长,根据其相等求得x的值即可;
(2)当PQ∥BC时,根据平行线分线段成比例定理,可得出关于AP,PQ,AB,AC的比例关系式,我们可根据P,Q的速度,用时间x表示出AP,AQ,然后根据得出的关系式求出x的值.
(3)本题要分两种情况进行讨论.已知了∠A和∠C对应相等,那么就要分成AP和CQ对应成比例以及AP和BC对应成比例两种情况来求x的值.
(1)依题意可得:BP=20-4x,CQ=3x
当BP=CQ时,20-4x=3x
∴![]() (秒)
(秒)
答:当![]() 秒时,BP=CQ
秒时,BP=CQ
(2)AP=4x,AB=20,AQ=30-3x,AC=30
所以当![]() 时,有
时,有![]()
即:![]()
解得:x=![]() (秒)
(秒)
答:当x=![]() 秒时,
秒时,![]() ;
;
(3)能.
①当△APQ∽△CQB时,有![]()
即:![]()
解得:x=![]() (秒)
(秒)
②当△APQ∽△CBQ时,有![]()
即:![]()
解得:x=5(秒)或x=-10(秒)(舍去)
答:当x=![]() 秒或x=5秒时,△APQ与△CQB相似.
秒或x=5秒时,△APQ与△CQB相似.

【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且利润率不得高于![]() .经市场调查,每天的销售量
.经市场调查,每天的销售量![]() (千克)与每千克售价
(千克)与每千克售价![]() (元)满足一次函数关系,部分数据如下表:
(元)满足一次函数关系,部分数据如下表:
售价 | 45 | 50 | 55 |
销售量 | 110 | 100 | 90 |
(1)求![]() 与
与![]() 之间的函数表达式,并写出自变量的范围;
之间的函数表达式,并写出自变量的范围;
(2)设每天销售该商品的总利润为![]() (元),求
(元),求![]() 与
与![]() 之间的函数表达式(利润=收入-成本),并求出售价为多少元时每天销售该商品所获得最大利润,最大利润是多少?
之间的函数表达式(利润=收入-成本),并求出售价为多少元时每天销售该商品所获得最大利润,最大利润是多少?
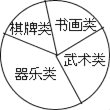
【题目】某校学生会准备调查六年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数.
(1)确定调查方式时,甲同学说:“我到六年级(1)班去调查全体同学”;乙同学说:“放学时我到校门口随机调查部分同学”;丙同学说:“我到六年级每个班随机调查一定数量的同学”.请指出哪位同学的调查方式最合理.
类别 | 频数(人数) | 频率 |
武术类 | 0.25 | |
书画类 | 20 | 0.20 |
棋牌类 | 15 | b |
器乐类 | ||
合计 | a | 1.00 |
(2)他们采用了最为合理的调查方法收集数据,并绘制了如图所示的统计表和扇形统计图.
请你根据以上图表提供的信息解答下列问题:
①a=_____,b=_____;
②在扇形统计图中,器乐类所对应扇形的圆心角的度数是_____;
③若该校六年级有学生560人,请你估计大约有多少学生参加武术类校本课程.