��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У����Dz����Ѻ��������������ȵĵ�С���֮�㡱������㣨1��1��������2����2����![]() �������ǡ���֮�㡱����Ȼ����֮�㡱����������
�������ǡ���֮�㡱����Ȼ����֮�㡱����������
��1������P��2��m���Ƿ���������y��![]() ��nΪ������n��0����ͼ���ϵġ���֮�㡱������������������Ľ���ʽ��
��nΪ������n��0����ͼ���ϵġ���֮�㡱������������������Ľ���ʽ��
��2������y��3kx+s��1��k��sΪ��������ͼ���ϴ��ڡ���֮�㡱�������ڣ����������֮�㡱�����꣬�������ڣ�˵�����ɣ�
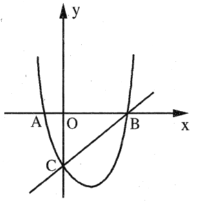
��3�������κ���y��ax2+bx+1��a��b�dz�����a��0����ͼ���ϴ�����������֮�㡱A��x1��x1����B��x2��x2���������㩁2��x1��2��|x1��x2|��2����t��b2��b+![]() ������t��ȡֵ��Χ��
������t��ȡֵ��Χ��
���𰸡���1��y��![]() ����2�����ڣ�����Ϊ��
����2�����ڣ�����Ϊ��![]() ��
��![]() ������3��t��
������3��t��![]() ��
��
��������
��1����������֮�����Ķ���ó�m��ֵ�����뷴���������Ľ���ʽ���n��ֵ���ɣ�
��2��������֮��ĺ���������������ͬ���ɵù���x�ķ��̣����ݽⷽ�̣��ɵô𰸣�
��3����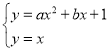 �ã�ax2+��b��1��x+1��0����x2��x2Ϊ�˷��̵���������ʵ������|x1��x2|��2�õ���2��x1��0ʱ������0��x1��2�õ���2��x2��4������������y��ax2+��b��1��x+1�ĶԳ���Ϊx��
�ã�ax2+��b��1��x+1��0����x2��x2Ϊ�˷��̵���������ʵ������|x1��x2|��2�õ���2��x1��0ʱ������0��x1��2�õ���2��x2��4������������y��ax2+��b��1��x+1�ĶԳ���Ϊx��![]() �����ǵõ���3��
�����ǵõ���3��![]() ��3�����ݶ��κ��������ʼ��ɵõ����ۣ�
��3�����ݶ��κ��������ʼ��ɵõ����ۣ�
�⣺��1���ߵ�P��2��m���Ƿ���������y��![]() ��nΪ������n��0����ͼ���ϵ�����֮������
��nΪ������n��0����ͼ���ϵ�����֮������
��m��2��
��P��2��2����
��n��2��2��4��
����������������Ľ���ʽΪy��![]() ��
��
��2����y��3kx+s��1�õ�y��xʱ����1��3k��x��s��1��
��k��![]() ��s��1ʱ��x���������⣬��ʱ������֮�������ڣ�����������
��s��1ʱ��x���������⣬��ʱ������֮�������ڣ�����������
��k��![]() ��s��1ʱ�������⣬��ʱ������֮���������ڣ�
��s��1ʱ�������⣬��ʱ������֮���������ڣ�
��k��![]() �����̵Ľ�Ϊx��
�����̵Ľ�Ϊx��![]() ����ʱ������֮�������ڣ�����Ϊ��
����ʱ������֮�������ڣ�����Ϊ��![]() ��
��![]() ����
����
��3����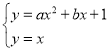 �ã�ax2+��b��1��x+1��0����x2��x2Ϊ�˷��̵���������ʵ����
�ã�ax2+��b��1��x+1��0����x2��x2Ϊ�˷��̵���������ʵ����
��|x1��x2|��2���֩�2��x1��2�ã���2��x1��0ʱ����4��x2��2��0��x1��2ʱ����2��x2��4��
��������y��ax2+��b��1��x+1�ĶԳ���Ϊx��![]() ���ʩ�3��
���ʩ�3��![]() ��3��
��3��
��|x1��x2|��2�����b��1��2��4a2+4a����a��![]() ��t��b2��b+
��t��b2��b+![]() ����b��1��2+
����b��1��2+![]() ��
��
y��4a2+4a+![]() ��4��a+
��4��a+![]() ��2+
��2+![]() ����a����
����a����![]() ʱ��t��a�����������a��
ʱ��t��a�����������a��![]() ʱ��t��
ʱ��t��![]() ��
��
��a��![]() ʱ��t��
ʱ��t��![]() ��
��

 ÿ��10���ӿ�����������������ϵ�д�
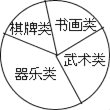
ÿ��10���ӿ�����������������ϵ�д�����Ŀ��ijУѧ�������������꼶ѧ���μӡ������ࡱ�����黭�ࡱ���������ࡱ���������ࡱ����У���γ̵�������
��1��ȷ�����鷽ʽʱ����ͬѧ˵�����ҵ����꼶��1����ȥ����ȫ��ͬѧ������ͬѧ˵������ѧʱ�ҵ�У�ſ�������鲿��ͬѧ������ͬѧ˵�����ҵ����꼶ÿ�����������һ��������ͬѧ������ָ����λͬѧ�ĵ��鷽ʽ�������
��� | Ƶ���������� | Ƶ�� |
������ | 0.25 | |
�黭�� | 20 | 0.20 |
������ | 15 | b |
������ | ||
�ϼ� | a | 1.00 |
��2�����Dz�������Ϊ�����ĵ��鷽���ռ����ݣ�����������ͼ��ʾ��ͳ�Ʊ�������ͳ��ͼ��
�����������ͼ���ṩ����Ϣ����������⣺
��a=_____��b=_____��
��������ͳ��ͼ�У�����������Ӧ���ε�Բ�ĽǵĶ�����_____��
������У���꼶��ѧ��560�ˣ�������ƴ�Լ�ж���ѧ���μ�������У���γ̣�