题目内容
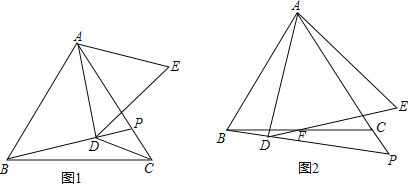
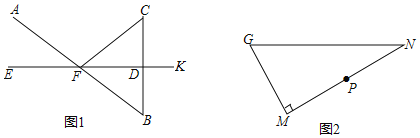
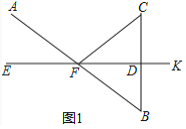
【题目】（1）如图1，已知EK垂直平分BC，垂足为D，AB与EK相交于点F，连接CF．求证：∠AFE=∠CFD．
（2）如图2，在Rt△GMN中，∠M=90°，P为MN的中点．
①用直尺和圆规在GN边上求作点Q，使得∠GQM=∠PQN（保留作图痕迹，不要求写作法）；
②在①的条件下，如果∠G=60°，那么Q是GN的中点吗？为什么？
【答案】(1)证明见解析；（2）①作图见解析；②结论：
是
的中点．理由见解析.
【解析】
（1）只要证明FC=FB即可解决问题；
（2）①作点P关于GN的对称点P′，连接P′M交GN于Q，连接PQ，点Q即为所求．
②结论：Q是GN的中点．想办法证明∠N=∠QMN=30°，∠G=∠GMQ=60°，可得QM=QN，QM=QG；
（1）证明：如图1中，
垂直平分线段
，
，
，
，
．
（2）①作点
关于的对称点
，连接
交于，连接
，点即为所求．
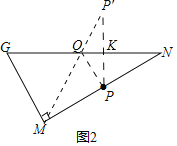
理由：
垂直平分
，
，
，
，
，
点即为所求．
②结论：是的中点．
理由：设交于
．
，
，
，
，
，
，
，
，
，
，
，
，
，
，
是的中点．
练习册系列答案
考前必练系列答案
相关题目
