Question

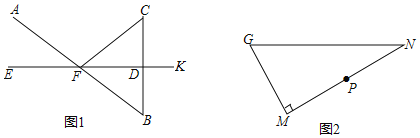
【题目】如图，抛物线与轴交于，，两点（点在点的左侧），与轴交于点，且，的平分线交轴于点，过点且垂直于的直线交轴于点，点是轴下方抛物线上的一个动点，过点作轴，垂足为，交直线于点．

（1）求抛物线的解析式；

（2）设点的横坐标为，当时，求的值；

（3）当直线为抛物线的对称轴时，以点为圆心，为半径作，点为上的一个动点，求的最小值．

Answer 1

【答案】（1）yx2x﹣3；（2）；（3）．

【解析】

对于（1），结合已知先求出点B和点C的坐标，再利用待定系数法求解即可；

对于（2），在Rt△OAC中，利用三角函数的知识求出∠OAC的度数，再利用角平分线的定义求出∠OAD的度数，进而得到点D的坐标；接下来求出直线AD的解析式，表示出点P，H，F的坐标，再利用两点间的距离公式可完成解答；对于（3），首先求出⊙H的半径，在HA上取一点K，使得HK=14，此时K（-，）；然后由HQ2=HK·HA，得到△QHK∽△AHQ，再利用相似三角形的性质求出KQ=AQ，进而可得当E、Q、K共线时，AQ+EQ的值最小，据此解答.

（1）由题意A（，0），B（﹣3，0），C（0，﹣3），设抛物线的解析式为y＝a（x+3）（x），把C（0，﹣3）代入得到a，∴抛物线的解析式为yx2x﹣3．

（2）在Rt△AOC中，tan∠OAC，∴∠OAC＝60°．

∵AD平分∠OAC，∴∠OAD＝30°，∴OD＝OAtan30°＝1，∴D（0，﹣1），∴直线AD的解析式为yx﹣1，由题意P（m，m2m﹣3），H（m，m﹣1），F（m，0）．

∵FH＝PH，∴1m﹣1﹣（m2m﹣3）

解得m或（舍弃），∴当FH＝HP时，m的值为．

（3）如图，∵PF是对称轴，∴F（，0），H（，﹣2）．

∵AH⊥AE，∴∠EAO＝60°，∴EOOA＝3，∴E（0，3）．

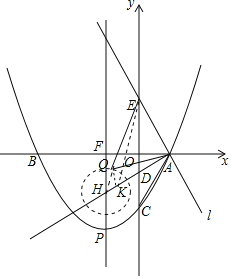
∵C（0，﹣3），∴HC2，AH＝2FH＝4，∴QHCH＝1，在HA上取一点K，使得HK，此时K（）．

∵HQ2＝1，HKHA＝1，∴HQ2＝HKHA，∴．

∵∠QHK＝∠AHQ，∴△QHK∽△AHQ，∴，∴KQAQ，∴AQ+QE＝KQ+EQ，∴当E、Q、K共线时，AQ+QE的值最小，最小值．