题目内容
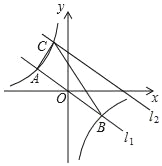
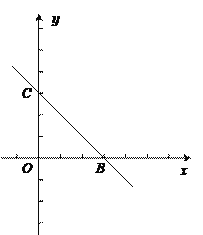
【题目】如图,在平面直角坐标系xOy中,直线BC与抛物线y=x2+bx+c交于点B(3,0)和点C(0,3),抛物线y=x2+bx+c过点B、C且与x轴的另一个交点为A.
(1)求直线BC及该抛物线的表达式;
(2)设该抛物线的顶点为D,求△DBC的面积.
【答案】(1)y=x2﹣4x+3(2)3
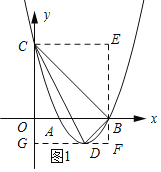
【解析】分析:(1)、利用待定系数法求出一次函数和抛物线的函数解析式;(2)、过点C作CE∥x轴,过点B作EF∥y轴,过点D作DF∥x轴,根据S△DBC=S四边形CEFG﹣S△CDG﹣S△BFD﹣S△BCE得出答案.
详解:(1)设直线BC的解析式y=kx+b(k≠0),将点B(3,0)C(0,3)代入得:
![]() 解得
解得![]() , ∴直线BC的解析式为y=﹣x+3.
, ∴直线BC的解析式为y=﹣x+3.
将B(3,0),C(0,3)代入抛物线的解析式得:![]() , 解得:b=﹣4,c=3,
, 解得:b=﹣4,c=3,
∴抛物线的解析式为y=x2﹣4x+3.
(2)如图1所示:过点C作CE∥x轴,过点B作EF∥y轴,过点D作DF∥x轴.
y=x2﹣4x+3=(x﹣2)2﹣1. ∴D(2,﹣1).
∴S△DBC=S四边形CEFG﹣S△CDG﹣S△BFD﹣S△BCE=12﹣![]() ×2×4﹣
×2×4﹣![]() ×1×1﹣
×1×1﹣![]() ×3×3=3.
×3×3=3.

练习册系列答案
相关题目