题目内容
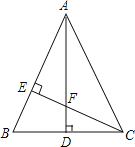
【题目】如图,CD和BE是△ABC的两条高,∠BCD=45°,BF=FC,BE与DF、DC分别交于点G、H,∠ACD=∠CBE.
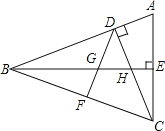
(1)判断△ABC的形状并说明理由;
(2)小明说:BH的长是AE的2倍.你认为正确吗?请说明理由.
(3)若BG=n2+1,GE=n2﹣1,求BH的长.
【答案】(1)等腰三角形,理由见解析;(2)正确,理由见解析;(3)BH=4n.
【解析】
试题分析:(1)由CD和BE是△ABC的两条高,于是得到∠A=∠ACD+∠A=90°,于是得到∠ABE=∠ACD,由于∠ACD=∠CBE,折叠∠ABE=∠CBE,通过△BAE≌△BCE,根据全等三角形的性质得到BA=BC,于是得到结论;
(2)根据等腰直角三角形的性质得到BD=DC证得△BDH≌△CDA,根据全等三角形的性质得到BH=AC,根据直角三角形的性质得到AC=2AE,BH=2AE,即可得到结论;
(3)连接GC,根据勾股定理列方程即可得到结论.
解:(1)∵CD和BE是△ABC的两条高,
∴∠A=∠ACD+∠A=90°,
∴∠ABE=∠ACD,
∵∠ACD=∠CBE,
∴∠ABE=∠CBE,
∵∠BEA=∠BEC=90°,
在△BAE与△BCE中,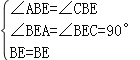 ,
,
∴△BAE≌△BCE,
∴BA=BC,
∴△ABC是等腰三角形;
(2)∵∠BDC=90°,∠BCD=45°,
∴BD=DC,
∵∠BDH=∠CDA=90°,
在△BDH与△CDA中,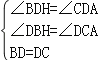 ,
,
∴△BDH≌△CDA,
∴BH=AC,
∵BE⊥AC,
∴AC=2AE,
BH=2AE,
∴小明说的正确;
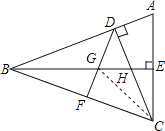
(3)连接GC,则GC=BG=n2+1,
在Rt△GEC中,
CE2=GC2﹣GE2=(n2+1)2﹣(n2﹣1)2=4n2,
∴CE=2n,
∴AC=2CE=4n,
∴BH=4n.

练习册系列答案
相关题目