题目内容
【题目】在数学实验课上，李静同学剪了两张直角三角形纸片，进行如下的操作：
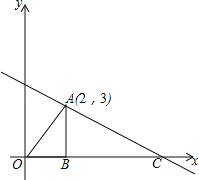
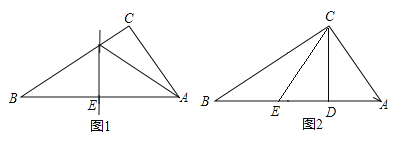
操作一：如图1，将Rt△ABC纸片沿某条直线折叠，使斜边两个端点A与B重合，折痕为DE．
（1）如果AC＝5cm，BC＝7cm，可得△ACD的周长为 ；
（2）如果∠CAD：∠BAD=1：2，可得∠B的度数为 ；
操作二：如图2，李静拿出另一张Rt△ABC纸片，将直角边AC沿直线CD折叠，使点A与点E重合，若AB＝10cm，BC＝8cm，请求出BE的长．
【答案】操作（一）（1）12cm．（2）36°；操作（二）：2.8cm.
【解析】试题分析：操作一：（1）由翻折的性质可知：BD=AD，于是AD+DC=BC，从而可知△ACD的周长=BC+AC；
（2）设∠CAD=x，则∠BAD=2x，由翻折的性质可知∠CBA=2x，然后根据直角三角形两锐角互余可知：x+2x+2x=90°．
操作二：先利用勾股定理求得AC的长，然后利用面积法求得DC的长，在Rt△ACD中，利用勾股定理可求得AD的长，由翻折的性质可知：DE=DA，最后根据BE=AB﹣DE﹣AD计算即可．
解：操作一：（1）翻折的性质可知：BD=AD，
∴AD+DC=BC=7．
∴△ACD的周长=CD+AD+AC=BC+AC=7+5=12cm．
故答案为：12cm．
（2）设∠CAD=x，则∠BAD=2x．
由翻折的性质可知：∠BAD=∠CBA=2x，
∵∠B+∠BAC=90°，
∴x+2x+2x=90°．
解得；x=18°．
∴2x=2×18°=36°．
∴∠B=36°．
故答案为：36°．
操作二：在Rt△ABC中，AC=
=6．
由翻折的性质可知：ED=AD，DC⊥AB．
∵
，
∴10CD=6×8．
∴CD=4.8．
在Rt△ADC中，AD=
=
=3.6．
∴EA=3.6×2=7.2．
∴BE=10﹣7.2=2.8．
