题目内容
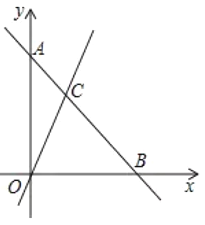
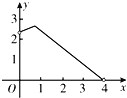
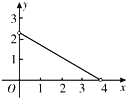
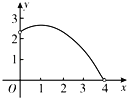
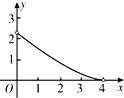
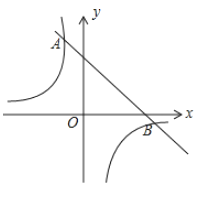
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于
的图象相交于![]() ,
,![]() 两点,其中点
两点,其中点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)根据函数图象,直接写出满足![]() 的
的![]() 的取值范围是_______;
的取值范围是_______;
(2)求这两个函数的表达式;
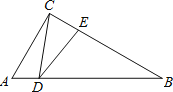
(3)点![]() 在线段
在线段![]() 上,且
上,且![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)-1<x<0或x>3;(2)y=![]() ,y=x+2;(3)(
,y=x+2;(3)(![]() ,
,![]() )
)
【解析】
(1)由题意得出反比例函数的图象总在一次函数的图象上方,即可得出结果;
(2)先把点A点坐标代入![]() 中求出k2得到反比例函数解析式为y=
中求出k2得到反比例函数解析式为y=![]() ;再把B(3,n)代入y=
;再把B(3,n)代入y=![]() 中求出n得到得B(3,1),然后利用待定系数法求一次函数解析式;
中求出n得到得B(3,1),然后利用待定系数法求一次函数解析式;
(3)设P(x,x+2),利用三角形面积公式得到AP:PB=2:3,即2PB=3PA,根据两点间的距离公式得到4[(x3)2+(x+2+1)2]=9[(x+1)2+(x+23)2],然后解方程求出x即可得到P点坐标.
解:(1)若![]() ,则反比例函数的图象总在一次函数的图象上方,
,则反比例函数的图象总在一次函数的图象上方,
∴-1<x<0或x>3.
故答案为:-1<x<0或x>3.
(2)把点A(1,3)代入![]() 得k2=1×3=3,
得k2=1×3=3,
∴反比例函数解析式为y=![]() ;
;
把B(3,n)代入 y=![]() 得3n=3,
得3n=3,
解得n=1,则B(3,1),
把A(1,3),B(3,1)代入y=k1x+b得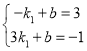 ,
,
解得![]() ,
,
∴一次函数解析式为y=x+2;
(3)设P(x,x+2),
∵![]() ,
,
∴AP:PB=2:3,
即2PB=3PA,
∴4[(x3)2+(x+2+1)2]=9[(x+1)2+(x+23)2],
解得x1=![]() ,x2=9(舍去),
,x2=9(舍去),
∴P点坐标为(![]() ,
,![]() ).
).

【题目】某校为了预测本校九年级男生毕业体育测试达标情况,随机抽取该年级部分男生进行了一次测试(满分50分,成绩均记为整数分),并按测试成绩![]() (单位:分)分成四类:
(单位:分)分成四类:![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),
),![]() 类(
类(![]() )绘制出如图所示的不完整条形统计图,请根据图中信息解答下列问题:
)绘制出如图所示的不完整条形统计图,请根据图中信息解答下列问题:
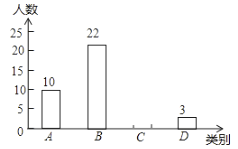
成绩等级 | 人数 | 所占百分比 |
| 10 |
|
| 22 |
|
|
|
|
| 3 |
|
(1)![]() ______,
______,![]() _______,
_______,![]() _________;
_________;
(2)补全条形统计图;
(3)若该校九年级男生有600名,![]() 类为测试成绩不达标,请估计该校九年级男生毕业体育测试成绩能达标的有多少名?
类为测试成绩不达标,请估计该校九年级男生毕业体育测试成绩能达标的有多少名?