Question

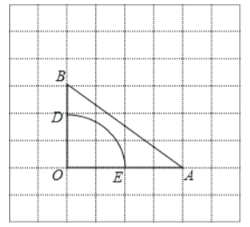
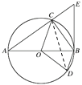
【题目】如图，AB为⊙O的直径，点D是AB下方圆上的一点，点C是优弧AD的中点，过点B作⊙O的切线BE交AC的延长线于点E，连接OC，OD，CB，BD．

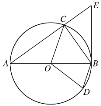
（1）求证：BD∥OC；

（2）当AB＝6时，完成填空：

①当BE＝ 时，四边形ODBC是菱形；

②当BE＝ 时，S△BCE＝S△ABC．

Answer 1

【答案】（1）见解析；（2）①； ②3

【解析】

（1）连接CD，根据圆的基本性质可得AC＝DC，然后证出≌，可得∠A＝∠ODC，然后根据同弧所对的圆周角性质可得∠A＝∠CDB，再推出∠OCD＝∠CDB即可证出结论；

（2）①根据切线的性质可得∠ABE=90°，当AB＝6，BE＝时，利用锐角三角函数即可求出∠A，从而求出∠COB和∠ODB，根据等边三角形的判定定理可证和都是等边三角形，从而得出BC=OC=OD=BD，即可证出结论；

②根据切线的性质可得∠ABE=90°，当AB＝6，BE＝3时，利用锐角三角函数即可求出tanA，从而得出，设BC=x，利用勾股定理求出BC和AC，再利用勾股定理即可求出CE，即可求出CE：AC，然后根据两个三角形等高时，面积比等于底之比即可得出结论．

（1）证明：连接CD，

∵点C为优弧AD的中点，

∴AC＝DC．

又∵OA＝OD，OC＝OC，

∴≌，

∴∠A＝∠ODC．

又∵∠A与∠CDB都为所对的圆周角，

∴∠A＝∠CDB，

∴∠ODC＝∠CDB．

∵OD＝OC，

∴∠ODC＝∠OCD，

∴∠OCD＝∠CDB

∴BD∥OC．

（2）解：①当BE＝时，四边形ODBC是菱形，理由如下

∵BE为⊙O的切线

∴∠ABE=90°

当AB＝6，BE＝时，

∴tanA=

∴∠A=30°

∴∠COB=2∠A=60°，∠ODB=∠ODC＋∠CDB=2∠A=60°

∵OC =OB=OD

∴和都是等边三角形

∴BC=OC=OD=BD

∴四边形ODBC是菱形

故答案为：；

②当BE＝3时，S△BCE＝S△ABC，理由如下

∵BE为⊙O的切线

∴∠ABE=90°

当AB＝6，BE＝3时，

∴tanA=

∵AB为直径

∴∠ACB=90°

∴tanA=

设BC=x，则AC=2x

∴BC2+AC2=AB2

即x2+（2x）2=62

解得：x=或（不符合实际，舍去）

∴BC=，AC=

在Rt△BCE中，CE=

∴CE：AC=：=1：4

∴S△BCE：S△ABC=1：4

∴S△BCE＝S△ABC．

故答案为：3 ．