题目内容
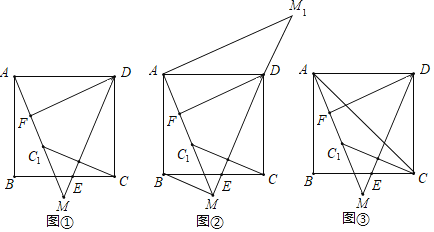
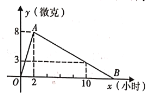
【题目】如图（1），直线l的解析式为y＝－x＋b，且与x轴，y轴分别交于点A、B．平行于直线l的直线m从原点O出发，沿x轴的正方向以每秒1个单位长度的速度运动，与x轴，y轴分别交于点C，D，运动时间为t秒（0≤t≤b），将△OCD沿着直线m翻折得到△ECD．若△ECD和△OAB的重合部分的面积为S（设t＝0或b时，S＝0），且S与t之间的函数关系的图象如图（2）所示，则图象中的最高点P的坐标是（ ）
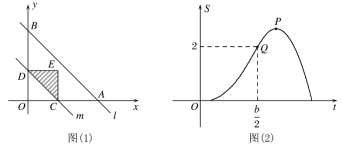
A.（
，3）B.（3，3）C.（，）D.（3，）
【答案】C
【解析】
先根据（
，2）求出直线的解析式，再根据解析式求出A、B的坐标，计算
的面积，然后用t表示出重合部分的面积，根据题意列出方程即可得到答案．
在题干图１位置，S△MNP=
t2，将（ ，2）代入S△MNP=t2，得： 
，解得
（负值舍去），
即直线l的解析式为y＝－x＋４．
所以，A（4，0），B（0，4）．
所以，S△ABO=OA·OB=×4×4=8，
如图，当0＜t≤2时，S△MNP=t2，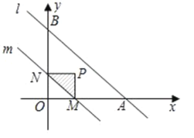
当t=2时，S△MNP最大，S△MNP=t2=×22=2，
如图，当2＜t≤4时，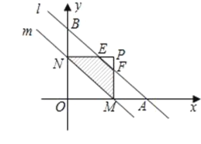
S1=S△ABO-S△OMN-2S△MAF，
即S1=
=
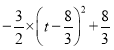
当
时，S1最大=
，
因为S1＞S△MNP，
所以此时为面积的最大值，则最高点P的坐标（，）
故选：C
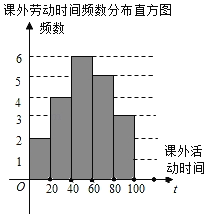
名校课堂系列答案【题目】遵义市各校都在深入开展劳动教育，某校为了解七年级学生一学期参加课外劳动时间（单位：h）的情况，从该校七年级随机抽查了部分学生进行问卷调查，并将调查结果绘制成如下不完整的频数分布表和频数分布直方图．
课外劳动时间频数分布表
劳动时间分组 | 频数 | 频率 |
0≤t＜20 | 2 | 0.1 |
20≤t＜40 | 4 | m |
40≤t＜60 | 6 | 0.3 |
60≤t＜80 | a | 0.25 |
80≤t＜100 | 3 | 0.15 |
解答下列问题：
（1）频数分布表中a＝ ，m＝ ；将频数分布直方图补充完整；
（2）若七年级共有学生400人，试估计该校七年级学生一学期课外劳动时间不少于60h的人数；
（3）已知课外劳动时间在60h≤t＜80h的男生人数为2人，其余为女生，现从该组中任选2人代表学校参加“全市中学生劳动体验”演讲比赛，请用树状图或列表法求所选学生为1男1女的概率．
