��Ŀ����
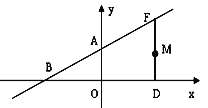
����Ŀ����һ����ֱ�Ĺ�·����A��B��C���أ�A����B��C����֮�䣮�ס������������ֱ��B��C����ͬʱ��������������·����������ʻ����������ʻ1Сʱ����A�غ��������ͬ���ٶ���C����ʻ������C��ֹͣ����������ʻ1.2Сʱ��A�ز�ֹͣ�˶����ס���������A�صľ���y1��y2��ǧ�ף�����ʻʱ��x��ʱ���ĺ�����ϵ��ͼ��ʾ��
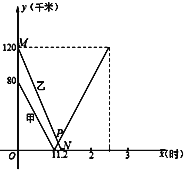
(1)BC�ľ���Ϊ km
�����߶�MN�ĺ�������ʽ��
�����P�����꣬��˵����P��ʵ�����壻
�������ʱ��������������60km��
���𰸡���1��200����2��y=-100x+120����3��![]() ��(4)
��(4) ![]() .
.
��������
��1���۲�ͼ�ɵó�BC�ľ��룻
��2�����ݺ���ͼ���е����ݿ�������߶�MN�ĺ�������ʽ��
��3����������ͺ���ͼ���е����ݿ�����õ�P�����꣬��˵����P��ʵ�����壻
��4�����ҳ�����A��֮ǰ���60km�͵���A��֮�����60km�����
��1����ͼ�ɵó�BC�ľ���Ϊ80+120=200km��
�ʴ�Ϊ��200��
��2�����߶�MN�ĺ�������ʽΪy=kx+b��
![]() �����
�����![]() ��
��
���߶�MN�ĺ�������ʽΪy=-100x+120��
��2����v��=80��1=80��v��=120��1.2=100��
����120+80���£�100+80��=![]() ��
��
��x=![]() ����y=-100x+120����y=
����y=-100x+120����y=![]() ��
��
���P��������![]() ��
��![]() ����
����
��P��ʵ�������ʾ��ʻ��![]() Сʱ�ס���������������ʱ��A�صľ���Ϊ
Сʱ�ס���������������ʱ��A�صľ���Ϊ![]() ǧ�ף�
ǧ�ף�
��4�������xСʱ�ס������60km��
�����������
���ҳ�����A��֮ǰ����Ϊ60 km��������ã�80+100��x+60=200��
���x=![]() ��
��
���ҳ�����A��֮�����Ϊ60 km���������80x=80+60��
���x=![]() ��
��
���Գ���![]() ��
��![]() Сʱ�ס������60km.
Сʱ�ס������60km.