题目内容
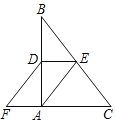
【题目】如图,![]() ,
,![]() ,点
,点![]() 在
在![]() 边上,
边上,![]() ,
,![]() 和
和![]() 相交于点
相交于点![]() .
.

(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)见解析(2)70![]()
【解析】
(1)根据全等三角形的判定即可判断△AEC≌△BED,即可求解;
(2)由(1)可知:EC=ED,∠C=∠BDE,根据等腰三角形的性质即可知∠C的度数,从而可求出∠BDE的度数.
(1)∵AE和BD相交于点O,
∴∠AOD=∠BOE.
在△AOD和△BOE中,
∠A=∠B,
∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO,
∴∠AEC=∠BED.
在△AEC和△BED中,
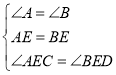 ,
,
∴△AEC≌△BED(ASA).∴ED=EC
(2)∵△AEC≌△BED,
∴EC=ED,∠C=∠BDE.
在△EDC中,
∵EC=ED,∠1=40![]() ,
,
∴∠C=∠EDC=70![]() ,
,
∴∠BDE=∠C=70![]() .
.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目