题目内容
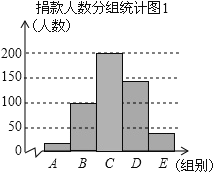
【题目】某校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图的统计图(图中信息不完整).已知A,B两组捐款人数的比为1∶5.
捐款人数分组统计表
组别 | 捐款额x/元 | 人数 |
A | 1≤x<10 | a |
B | 10≤x<20 | 100 |
C | 20≤x<30 | |
D | 30≤x<40 | |
E | x≥40 |
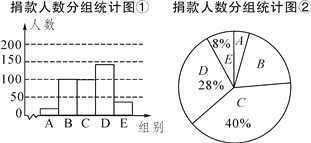
请结合以上信息解答下列问题:
(1)a=____,本次调查的样本容量是______;
(2)先求出C组的人数,再补全“捐款人数分组统计图①;
(3)若该学校自愿捐款的学生有1500人,请估计捐款不少于30元的学生有多少人?
【答案】 20 500 C组的人数为500×40%=200(人),补图略(3)540人
【解析】试题分析:(1)根据![]() 两组捐款的人数的比列式求解即可得到
两组捐款的人数的比列式求解即可得到![]() 的值,求出
的值,求出![]() 两组捐款人数所占的百分比的和与
两组捐款人数所占的百分比的和与![]() 两组捐款的人数的和,列式计算即可求出样本容量;
两组捐款的人数的和,列式计算即可求出样本容量;
(2)用样本容量乘以C组人数所占的百分比,计算即可得解,然后再补全统计图;
(3)先求出![]() 两组的人数的和,再根据概率公式列式计算即可,或直接求出
两组的人数的和,再根据概率公式列式计算即可,或直接求出![]() 两组捐款人数所占的百分比的和即可.
两组捐款人数所占的百分比的和即可.
试题解析:(1)∵A、B两组捐款人数的比为1:5,B组捐款人数为100人,
∴A组捐款人数为:100÷5=20,
A.B两组捐款人数所占的百分比的和为:140%28%8%=176%=24%,
A.B两组捐款的人数的和为:20+100=120,
120÷24%=500,
故答案为:20,500;
(2)500×40%=200,
C组的人数为200,
补图见图.
(3)∵D、E两组的人数和为:
1500×(28%+8%)=540,
即捐款不少于30元的学生估计有540人.

练习册系列答案
相关题目