题目内容
【题目】如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.

(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)连接OD,求出∠AOD,求出∠DOB,求出∠ODP,根据切线判定推出即可;
(2)求出OP、DP长,分别求出扇形DOB和三角形ODP面积,即可求出答案.
试题解析:(1)连接OD,
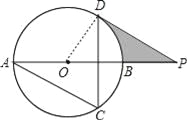
∵∠ACD=60°,
∴由圆周角定理得:∠AOD=2∠ACD=120°,
∴∠DOP=180°﹣120°=60°,
∵∠APD=30°,
∴∠ODP=180°﹣30°﹣60°=90°,
∴OD⊥DP,
∵OD为半径,
∴DP是⊙O切线;
(2)∵∠P=30°,∠ODP=90°,OD=3cm,
∴OP=6cm,由勾股定理得:DP=3![]() cm,
cm,
∴图中阴影部分的面积S=S△ODP﹣S扇形DOB=![]() ×3×3
×3×3![]() ﹣
﹣![]() cm2
cm2

 阅读快车系列答案
阅读快车系列答案【题目】某校举行“汉字听写”比赛,每位学生听写汉字![]() 个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
组别 | 正确字数 | 人数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

根据以上信息解决下列问题:
(1)在统计表中,![]() __________,
__________,![]() __________,并补全直方图;
__________,并补全直方图;
(2)扇形统计图中“![]() 组”所对应的圆心角的度数是__________度;
组”所对应的圆心角的度数是__________度;
(3)若该校共有![]() 名学生,如果听写正确的个数少于
名学生,如果听写正确的个数少于![]() 个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.
个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.
【题目】王老师将3个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出一个球(有放回),下表是活动进行中的一组部分统计数据.
摸球的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数 | 23 | 31 | 60 | 127 | 203 | 251 |
摸到黑球的频率 | 0.23 | 0.21 | 0.30 | 0.254 | 0.253 | ___ |
(1)根据上表数据计算![]() = .估计从袋中摸出一个球是黑球的概率是 .(精确到0. 01)
= .估计从袋中摸出一个球是黑球的概率是 .(精确到0. 01)
(2)估算袋中白球的个数.