题目内容
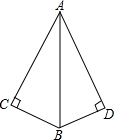
如图1,在△ABC与△BDE中,∠ABC=∠BDE=90°,BC=DE,AB=BD,M、M′分别为AB、BD中点.
(1)探索CM与EM′有怎样的数量关系?请证明你的结论;
(2)如图2,连接MM′并延长交CE于点K,试判断CK与EK之间的数量关系,并说明理由.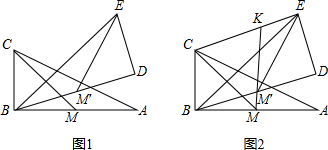
(1)探索CM与EM′有怎样的数量关系?请证明你的结论;
(2)如图2,连接MM′并延长交CE于点K,试判断CK与EK之间的数量关系,并说明理由.

(1)CM=EM′.
证明:根据线段中点的概念和已知的AB=BD,得BM=DM′;
在Rt△BCM与Rt△DEM′中,
,
∴Rt△BCM≌Rt△DEM′(HL),
∴CM=EM′;
(2)CK=KE.理由如下:
如图2,延长MK至L,使KL=MM',连接LE,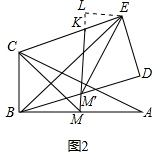
则KL+KM′=MM'+KM′,即KM=LM′,
由(1)可知CM=EM′,
∵BD=AB,M是AB的中点,M'是BD的中点,
∴BM=BM′,
∴∠BMM′=∠BM′M,
由(1)知Rt△BCM≌Rt△DEM′,
∴∠BMC=∠EM′D,
∴∠CMK=∠KM′E,
在△CMK和△EM′L中
∴△CMK≌△EM′L(SAS),
∴CK=EL,
又∵∠CKM=∠LKE=∠KLE,
∴KE=LE,
∴CK=KE.
证明:根据线段中点的概念和已知的AB=BD,得BM=DM′;
在Rt△BCM与Rt△DEM′中,
|
∴Rt△BCM≌Rt△DEM′(HL),
∴CM=EM′;
(2)CK=KE.理由如下:
如图2,延长MK至L,使KL=MM',连接LE,

则KL+KM′=MM'+KM′,即KM=LM′,
由(1)可知CM=EM′,
∵BD=AB,M是AB的中点,M'是BD的中点,
∴BM=BM′,
∴∠BMM′=∠BM′M,
由(1)知Rt△BCM≌Rt△DEM′,
∴∠BMC=∠EM′D,
∴∠CMK=∠KM′E,
在△CMK和△EM′L中
|
∴△CMK≌△EM′L(SAS),
∴CK=EL,
又∵∠CKM=∠LKE=∠KLE,
∴KE=LE,
∴CK=KE.

练习册系列答案
相关题目
 以1.5厘米∕秒的速度移动,点Q从点B开始沿BC边向C点以2厘米∕秒的速度移动.
以1.5厘米∕秒的速度移动,点Q从点B开始沿BC边向C点以2厘米∕秒的速度移动.