题目内容
【题目】【操作发现】
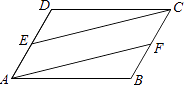
（1）如图1，
为等边三角形，先将三角板中的
角与
重合，再将三角板绕点
按顺时针方向旋转（旋转角大于
且小于
）.旋转后三角板的一直角边与
交于点
.在三角板斜边上取一点
，使
，线段
上取点
，使
，连接
，
.
①求
的度数；
②
与
相等吗？请说明理由；
【类比探究】
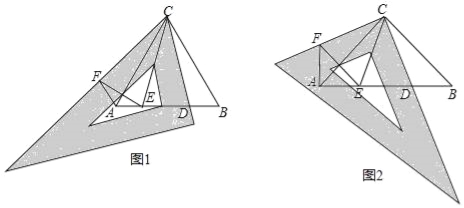
（2）如图2，
为等腰直角三角形，
，先将三角板的
角与重合，再将三角板绕点按顺时针方向旋转（旋转角大于且小于
）.旋转后三角板的一直角边与交于点.在三角板另一直角边上取一点
，使
，线段
上取点
，使
，连接，.请直接写出探究结果：
①的度数；
②线段
之间的数量关系.
【答案】(1)①120°；②DE=EF；理由见解析；（2）①90°；②AE2+DB2=DE2．理由见解析.
【解析】
试题分析：（1）①由等边三角形的性质得出AC=BC，∠BAC=∠B=60°，求出∠ACF=∠BCD，证明△ACF≌△BCD，得出∠CAF=∠B=60°，求出∠EAF=∠BAC+∠CAF=120°；
②证出∠DCE=∠FCE，由SAS证明△DCE≌△FCE，得出DE=EF即可；
（2）①由等腰直角三角形的性质得出AC=BC，∠BAC=∠B=45°，证出∠ACF=∠BCD，由SAS证明△ACF≌△BCD，得出∠CAF=∠B=45°，AF=DB，求出∠EAF=∠BAC+∠CAF=90°；
②证出∠DCE=∠FCE，由SAS证明△DCE≌△FCE，得出DE=EF；在Rt△AEF中，由勾股定理得出AE2+AF2=EF2，即可得出结论．
试题解析：（1）①∵△ABC是等边三角形，
∴AC=BC，∠BAC=∠B=60°，
∵∠DCF=60°，
∴∠ACF=∠BCD，
在△ACF和△BCD中，
，
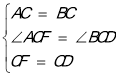∴△ACF≌△BCD（SAS），
∴∠CAF=∠B=60°，
∴∠EAF=∠BAC+∠CAF=120°；
②DE=EF；理由如下：
∵∠DCF=60°，∠DCE=30°，
∴∠FCE=60°﹣30°=30°，
∴∠DCE=∠FCE，
在△DCE和△FCE中，
，
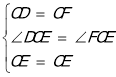∴△DCE≌△FCE（SAS），
∴DE=EF；
（2）①∵△ABC是等腰直角三角形，∠ACB=90°，
∴AC=BC，∠BAC=∠B=45°，
∵∠DCF=90°，
∴∠ACF=∠BCD，
在△ACF和△BCD中，
，
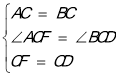∴△ACF≌△BCD（SAS），
∴∠CAF=∠B=45°，AF=DB，
∴∠EAF=∠BAC+∠CAF=90°；
②AE2+DB2=DE2，理由如下：
∵∠DCF=90°，∠DCE=45°，
∴∠FCE=90°﹣45°=45°，
∴∠DCE=∠FCE，
在△DCE和△FCE中，
，
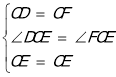∴△DCE≌△FCE（SAS），
∴DE=EF，
在Rt△AEF中，AE2+AF2=EF2，
又∵AF=DB，
∴AE2+DB2=DE2．
