Question

【题目】如图，在平行四边形ABCD中，点E、F分别是AD、BC的中点．求证：AF=CE．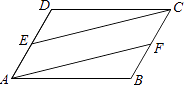

Answer 1

【答案】证明：∵四边形ABCD是平行四边形，

∴AD∥BC，AD=BC；

又∵点E、F分别是AD、BC的中点，

∴AE∥CF，AE=CF= AD，

∴四边形AECF为平行四边形（对边平行且相等的四边形为平行四边形），

∴AF=CE（平行四边形的对边相等）．

【解析】根据“平行四边形ABCD的对边平行且相等的性质”证得四边形AECF为平行四边形，然后由“平行四边形的对边相等”的性质证得结论．
【考点精析】通过灵活运用平行四边形的判定与性质，掌握若一直线过平行四边形两对角线的交点，则这条直线被一组对边截下的线段以对角线的交点为中点，并且这两条直线二等分此平行四边形的面积即可以解答此题．