题目内容
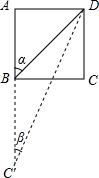 如图,已知正方形的边长为1,若将边BC绕点B旋转后,点C落在AB的延长线的C′处,连结C′D,设∠ABD=α,那么sinα+sinβ等于( )
如图,已知正方形的边长为1,若将边BC绕点B旋转后,点C落在AB的延长线的C′处,连结C′D,设∠ABD=α,那么sinα+sinβ等于( )分析:根据正方形的对角线平分一组对角可得∠ABD=45°,然后求出sinα,再根据旋转的性质求出BC′=BC=1,然后求出AC′,利用勾股定理列式求出C′D,再求出sinβ,然后相加即可得解.
解答:解:∵四边形ABCD是正方形,
∴α=∠ABD=45°,
∴sinα=
,
∵边BC绕点B旋转后,点C落在AB的延长线的C′处,
∴BC′=BC=1,
∴AC′=AB+BC′=1+1=2,
∴C′D=
=
,
∴sinβ=
=
=
,
∴sinα+sinβ=
+
=
.
故选D.
∴α=∠ABD=45°,
∴sinα=
| ||
| 2 |
∵边BC绕点B旋转后,点C落在AB的延长线的C′处,
∴BC′=BC=1,
∴AC′=AB+BC′=1+1=2,
∴C′D=
| 22+12 |
| 5 |
∴sinβ=
| AD |
| C′D |
| 1 | ||
|
| ||
| 5 |
∴sinα+sinβ=
| ||
| 2 |
| ||
| 5 |
5
| ||||
| 10 |
故选D.
点评:本题考查了正方形的性质,旋转的性质,勾股定理的应用,锐角三角函数,比较简单,熟记各性质是解题的关键.

练习册系列答案
相关题目

 如图:已知正方形的边长为a,三角形的高为h,此正方形剪去四个相同的三角形.
如图:已知正方形的边长为a,三角形的高为h,此正方形剪去四个相同的三角形. 如图,已知正方形的边长是4cm,求它的内切圆与外接圆组成的圆环的面积.(答案保留π)
如图,已知正方形的边长是4cm,求它的内切圆与外接圆组成的圆环的面积.(答案保留π) 如图,已知正方形的边长为x,用代数式表示图中阴影部分的面积S=
如图,已知正方形的边长为x,用代数式表示图中阴影部分的面积S= 如图,已知正方形的边长为2a,求阴影部分的面积,(用含a的代数式表示)
如图,已知正方形的边长为2a,求阴影部分的面积,(用含a的代数式表示) 如图,已知正方形的边长为a,以AB、CD为直径在正方形内画两个半圆,连接AC、BD.
如图,已知正方形的边长为a,以AB、CD为直径在正方形内画两个半圆,连接AC、BD.