Question

如图，已知正方形的边长为a，以AB、CD为直径在正方形内画两个半圆，连接AC、BD．
（1）用代数式表示阴影部分的面积；
（2）当a=4时，阴影部分的面积为多少？

Answer 1

分析：（1）半圆的面积减去△ABO的面积，然后乘以2即可求得阴影部分的面积；
（2）把a=4代入到（1）中的代数式即可化简求值．

解答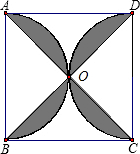：解：（1）半圆的面积是：

1

2

π（

a

2

）²=

πa2

8

；
则△ABO是等腰直角三角形，面积是：

1

2

×a•

a

2

=

a2

4

．
则阴影部分的面积是：2（

πa2

8

-

a2

4

）=

πa2-2a2

4

．
（2）当a=4时，阴影部分的面积是：

π×42-2×42

4

=4π-8．

点评：本题考查了列代数式以及代数式的求值，正确列出代数式是关键．