题目内容

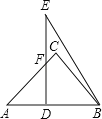
【题目】如图，将两块三角板重叠放置，其中∠C=∠BDE=90°，∠A=45°，∠E=30°，AB=DE=12．求重叠部分四边形DBCF的面积．

【答案】．

【解析】

观察可看出，所求四边形的面积等于等腰直角三角形的面积减去S△ADF，从而我们只要求出这两个三角形的面积即可，这要求我们综合利用解直角三角形，直角三角形的性质来解答．

设BD=x．

∵∠E=30°，∴BE=2DB=2x，DE==12，解得：x=4，∴DB= 4，∴AD=AB﹣DB=．

又∵∠A=45°，∠AFD=45°，∴FD=AD=，∴S△ADFAD2（）2=．

在等腰直角三角形ABC中，斜边AB=12，∴AC=BC=，∴S△ABCAC2=36，∴S四边形DBCF=S△ABC﹣S△ADF=36﹣（）=．

练习册系列答案
相关题目

【题目】如图所示，火车站、码头分别位于A，B两点，直线a和b分别表示铁路与河流．

（1）从火车站到码头怎样走最近，画图并说明理由；

（2）从码头到铁路怎样走最近，画图并说明理由；

（3）从火车站到河流怎样走最近，画图并说明理由．

【题目】如图，△ABC是⊙O的内接三角形，AB＝AC，∠BCA＝65°，作CD∥AB，并与○O相交于点D，连接BD，则∠DBC的大小为

A. 15° B. 35° C. 25° D. 45°

【题目】如图，可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域，其中标有数字“1”的扇形圆心角为120°．转动转盘，待转盘自动停止后，指针指向一个扇形的内部，则该扇形内的数字即为转出的数字，此时，称为转动转盘一次（若指针指向两个扇形的交线，则不计转动的次数，重新转动转盘，直到指针指向一个扇形的内部为止）

(1)转动转盘一次，求转出的数字是－2的概率；

(2)转动转盘两次，用树状图或列表法求这两次分别转出的数字之积为正数的概率．

【题目】问题提出

(1)如图①，在△ABC中，∠A＝120°，AB＝AC＝5，则△ABC的外接圆半径R的值为 ．

问题探究

(2)如图②，⊙O的半径为13，弦AB＝24，M是AB的中点，P是⊙O上一动点，求PM的最大值．

问题解决

(3)如图③所示，AB、AC、BC是某新区的三条规划路其中，AB＝6km，AC＝3km，∠BAC＝60°，BC所对的圆心角为60°．新区管委会想在BC路边建物资总站点P，在AB、AC路边分别建物资分站点E、F．也就是，分别在、线段AB和AC上选取点P、E、F．由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输，因此，要在各物资站点之间规划道路PE、EF和FP．为了快捷环保和节约成本要使得线段PE、EF、FP之和最短，试求PE＋EF＋FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计)．

图① 图② 图③

【题目】某次篮球联赛初赛阶段，每队有场比赛，每场比赛都要分出胜负，每队胜一场得分， 负一场得分，积分超过分才能获得参赛资格.

（1）已知甲队在初赛阶段的积分为分，求甲队初赛阶段胜、负各多少场；

（2）如果乙队要获得参加决赛资格，那么乙队在初赛阶段至少要胜多少场？

【题目】当涂大青山有较为丰富的毛竹资源，某企业已收购毛竹110吨，根据市场信息，将毛竹直接销售，每吨可获利100元；如果对毛竹进行粗加工，每天可加工8吨，每吨可获利1000元；如果进行精加工，每天可加工吨，每吨可获利5000元，由于受条件限制，在同一天中只能采用一种方式加工，并且必须在一个月（30天）内将这批毛竹全部销售、为此研究了两种方案：

（1）方案一：将收购毛竹全部粗加工后销售，则可获利________元；

方案二：30天时间都进行精加工，未来得及加工的毛竹，在市场上直接销售，则可获利________元．

（2）是否存在第三种方案，将部分毛竹精加工，其余毛竹粗加工，并且恰好在30天内完成？若存在，求销售后所获利润；若不存在，请说明理由．

【题目】已知：线段厘米．

（1）如图一，点沿线段自点向点以4厘米/分的速度运动，同时点沿线段自点向点以6厘米/分的速度运动．求：①几分钟后两点相遇？ ②几分钟后两点相距20厘米？

（2）如图二，厘米，，现将点绕着点以20度/分的速度顺时针旋转一周后停止，同时点沿直线自点向点运动，假若两点也能相遇，求点的速度．

【题目】如图,CA⊥BC,垂足为C,AC=2Cm,BC=6cm,射线BM⊥BQ,垂足为B,动点P从C点出发以1cm/s的速度沿射线CQ运动,点N为射线BM上一动点,满足PN=AB,随着P点运动而运动,当点P运动_______秒时，△BCA与点P、N、B为顶点的三角形全等.(2个全等三角形不重合)

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网