Question

【题目】（问题发现）

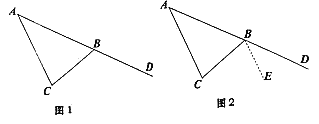
如图1，D是△ABC边AB延长线上一点，求证:∠A+∠C=∠CBD.

小白同学的想法是，过点B作 BE∥AC，从而将∠A和∠C转移到∠CBD处，使这三个角有公共顶点B，请你按照小白的想法，完成解答；

（问题解决）

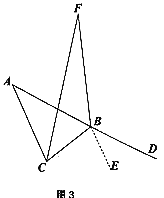
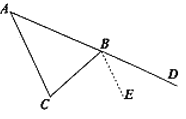
在上述问题的前提，,如图3，从点B引一条射线与∠ACB的角平分线交于点F，且∠CBF=∠D

BF，探究∠A与∠F的数量关系。在小白想法的提示下，小黑同学也想通过作平行线将∠A或∠F的位置进行转移，使两角有公共顶点,，请你根据小黑的想法或者学过的知识解决此问题。

Answer 1

【答案】问题发现:见解析. 问题解决:∠A与∠F的数量关系是∠F＝∠A,见解析。

【解析】

先根据两直线平行，同位角相等，内错角相等.得∠CBE=∠C，∠DBE=∠A再根据∠CBD=∠CBE+∠DBE即可得出结论．

根据角平分线及外角定理可得∠5=（∠A+2∠1）再化简即可得∠F＝∠A.

解：问题发现:

∵BE∥AC，
∴∠CBE=∠C，∠DBE=∠A．

∴∠CBD=∠CBE+∠DBE=∠A+∠C．
问题解决:

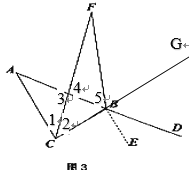
如图：延长CB至G，

∵∠CBF=∠DBF，∠CBA=∠DBG

∠5=∠GBF

∵CF为∠ACB的内角平分线，

∴∠1=∠2，

∵∠GBA=∠ACB+∠A

∴∠5=（∠A+2∠1），

∵∠3=∠4，∠A=180°-∠1-∠3

∴∠F=180°-∠4-∠5=180°-∠3-（∠A+2∠1）＝180°-∠3-∠1∠A
即∠F=∠A∠A＝∠A．

所以，∠A与∠F的数量关系是∠F＝∠A．