Question

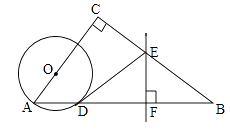
【题目】如图，已知AB是⊙O的直径，AD、BD是半圆的弦，∠PDA=∠PBD，∠BDE=60°，若PD= ，则PA的长为 ．

Answer 1

【答案】1
【解析】解：∵AB为直径，
∴∠ADB=90°，
∵∠BDE=60°，
∴∠PDA=180°﹣90°﹣60°=30°，
∴∠PBD=∠PDA=30°，
∵OB=OD，
∴∠ODB=∠PBD=30°，
∴∠ADO=60°，
∴△ADO为等边三角形，∠ODP=90°，
∴AD=OA，∠AOD=60°，PD为⊙O的切线，
∴∠P=30°，
∴PA=AD，PD2=PAPB，
∴ =PA3PA
∴PA=1；
所以答案是：1．
【考点精析】本题主要考查了圆周角定理和切线的性质定理的相关知识点，需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半；切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题．