题目内容
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP,CP的延长线分别交AD于点E,F,连结BD,DP,BD与CF相交于点H.给出下列结论: ①△ABE≌△DCF;②△DPH是等腰三角形;③PF= ![]() AB;④
AB;④ ![]() =
= ![]() .
.
其中正确结论的个数是( )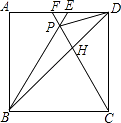
A.1
B.2
C.3
D.4
【答案】D
【解析】解:∵△BPC是等边三角形, ∴BP=PC=BC,∠PBC=∠PCB=∠BPC=60°,
在正方形ABCD中,
∵AB=BC=CD,∠A=∠ADC=∠BCD=90°
∴∠ABE=∠DCF=30°,
在△ABE与△CDF中,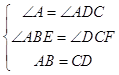 ,
,
∴△ABE≌△DCF,故①正确;
∵PC=DC,∠PCD=30°,
∴∠CPD=75°,
∵∠DBC=45°,∠BCF=60°,
∴∠DHP=∠BHC=75°,
∴PD=DH,
∴△DPH是等腰三角形,故②正确;
∵△BPC是等边三角形,
∴可得∠FPE=∠PFE=60°,
∴△FEP是等边三角形,
∴△FPE∽△CPB,
∴ ![]() =
= ![]() ,
,
设PF=x,PC=y,则DC=y,
∵∠FCD=30°,
∴y= ![]() (x+y),
(x+y),
整理得:(1﹣ ![]() )y=
)y= ![]() x,
x,
解得: ![]() =
= ![]() ,
,
则PF= ![]() AB,故③正确;
AB,故③正确;
如图,过P作PM⊥CD,PN⊥BC,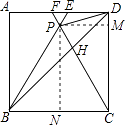
设正方形ABCD的边长是4,△BPC为正三角形,
∴∠PBC=∠PCB=60°,PB=PC=BC=CD=4,
∴∠PCD=30°
∴PN=PBsin60°=4× ![]() =2
=2 ![]() ,PM=PCsin30°=2,
,PM=PCsin30°=2,
S△BPD=S四边形PBCD﹣S△BCD=S△PBC+S△PDC﹣S△BCD
= ![]() ×4×2
×4×2 ![]() +
+ ![]() ×2×4﹣
×2×4﹣ ![]() ×4×4
×4×4
=4 ![]() +4﹣8=4
+4﹣8=4 ![]() ﹣4,
﹣4,
∴ ![]() =
= ![]() ,故④正确;
,故④正确;
故正确的有4个,
故选:D.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目