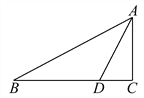
题目内容
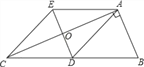
【题目】如图，△ABC是等腰三角形，且AC＝BC，∠ACB＝120°，在AB上取一点O，使OB＝OC，以点O为圆心，OB为半径作圆，过点C作CD∥AB交⊙O于点D，连接BD.
(1)猜想AC与⊙O的位置关系，并证明你的猜想；
(2)试判断四边形BOCD的形状，并证明你的判断；
(3)已知AC＝6，求扇形OBC所围成的圆锥的底面圆的半径r.
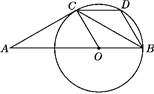
【答案】(1)猜想：AC与⊙O相切(2)四边形BOCD为菱形(3)
【解析】试题分析：本题考查了切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线．也考查了菱形的判定方法和圆锥的计算．（1）根据等腰三角形的性质得∠A=∠ABC=30°，再由OB=OC得∠OCB=∠OBC=30°，所以∠ACO=∠ACB-∠OCB=90°，然后根据切线的判定定理即可得到，AC是⊙O的切线；
（2）连结OD，由CD∥AB得到∠AOC=∠OCD，根据三角形外角性质得∠AOC=∠OBC+∠OCB=60°，所以∠OCD=60°，于是可判断△OCD为等边三角形，则CD=OB=OC，先可判断四边形OBDC为平行四边形，加上OB=OC，于是可判断四边形BOCD为菱形；（3）在Rt△AOC中，根据含30度的直角三角形三边的关系得到
OC=
∴弧BC的弧长=
然后根据圆锥的计算求圆锥的底面圆半径．
试题解析（1）AC与⊙O相切
，∠ACB＝120°，∴∠ABC＝∠A＝30°。
，∠CBO＝∠BCO＝30°，
∴∠OCA＝120°－30°＝90°，∴AC⊥OC，
又∵OC是⊙O的半径，
∴AC与⊙O相切。
（2）四边形BOCD是菱形
连接OD。
∵CD∥AB，
∴∠OCD＝∠AOC＝2×30°＝60°
，
∴△COD是等边三角形，
，
∴四边形BOCD是平行四边形，
∴四边形BOCD是菱形。
（3）在Rt△AOC中，∠A＝30°，AC＝6，
ACtan∠A＝6tan30°＝
，
∴弧BC的弧长
∴底面圆半径
