题目内容
【题目】如图,已知⊙O 中,AB为直径,CD为⊙O的切线,交AB的延长线于点D,∠D=30°.(1)求∠A的度数;(2)若点F在⊙O上,CF⊥AB,垂足为E,CF=4![]() ,求图中阴影部分的面积.(结果保留π)
,求图中阴影部分的面积.(结果保留π)

【答案】(1)∠A=30°;(2)![]() π﹣2
π﹣2![]() .
.
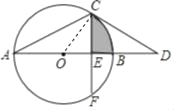
【解析】试题分析:(1)连接OC,如图,利用切线的性质得![]() 则利用互余可计算出
则利用互余可计算出![]() 然后根据等腰三角形的性质和三角形外角性质可求出∠A的度数;
然后根据等腰三角形的性质和三角形外角性质可求出∠A的度数;
(2)根据垂径定理得到![]() 再在
再在![]() 中利用解直角三角形求出
中利用解直角三角形求出![]() 的长,然后根据扇形面积公式,利用图中阴影部分的面积=S扇形BOC-S△OCE进行计算即可.
的长,然后根据扇形面积公式,利用图中阴影部分的面积=S扇形BOC-S△OCE进行计算即可.
试题解析:(1)连接OC,如图,
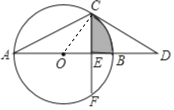
∵CD为⊙O的切线,
∴OC⊥CD,
∴![]()
∴![]()
∵OA=OC,
∴∠A=∠OCA,
而∠DOC=∠A+∠OCA,
∴![]()
(2)∵CF⊥AB,
∴![]()
在Rt△OCE中, ![]()
∴![]()
∴OC=2OE=4,
∴图中阴影部分的面积=S扇形BOCS△OCE![]()

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
【题目】甲、乙两名射击选手在10次射击训练中的成绩统计图(部分)如图所示:
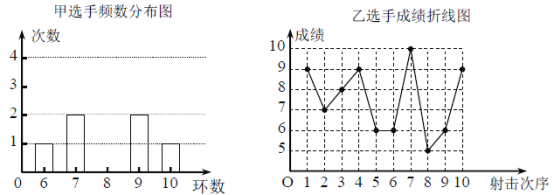
教练根据甲、乙两名射击选手的成绩绘制了如下数据分析表:
选手 | 平均数 | 中位数 | 众数 | 方差 |
甲 |
| 8 | 8 | c |
乙 | 7. 5 |
| 6和9 | 2. 65 |
根据以上信息,请解答下面的问题:
(1)补全甲选手10次成绩频数分布图;
(2)求![]() 的值;
的值;
(3)教练根据两名选手的10次成绩,决定选择甲选手参加射击比赛,教练的理由是什么?(至少从两个不同角度说明理由).