题目内容
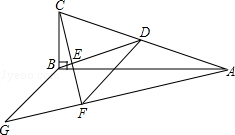
如图，
ABCD的周长为36，对角线AC，BD相交于点O．点E是CD的中点，BD=12，则△DOE的周长为 ．
ABCD的周长为36，对角线AC，BD相交于点O．点E是CD的中点，BD=12，则△DOE的周长为 ．15。
∵
ABCD的周长为36，∴2（BC+CD）=36，则BC+CD=18。
∵四边形ABCD是平行四边形，对角线AC，BD相交于点O，BD=12，∴OD=OB=BD=6。
又∵点E是CD的中点，∴OE是△BCD的中位线，DE=CD。∴OE=BC。
∴△DOE的周长="OD+OE+DE=" OD +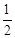
（BC+CD）=6+9=15，即△DOE的周长为15。
ABCD的周长为36，∴2（BC+CD）=36，则BC+CD=18。∵四边形ABCD是平行四边形，对角线AC，BD相交于点O，BD=12，∴OD=OB=BD=6。
又∵点E是CD的中点，∴OE是△BCD的中位线，DE=CD。∴OE=BC。
∴△DOE的周长="OD+OE+DE=" OD +
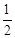（BC+CD）=6+9=15，即△DOE的周长为15。
练习册系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
相关题目
ABCD的周长为
，AC、BD相交于点O，OE⊥AC交AD于E，则△DCE的周长为( )
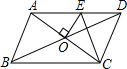
B、6
