Question

【题目】如图,已知二次函数 的图象过点,一次函数 的图象经过点.

（1）求值并写出二次函数表达式；

（2）求值；

（3）设直线与二次函数图象交于两点,过作垂直轴于点,

试证明:；

（4）在（3）的条件下，请判断以线段为直径的圆与轴的位置关系,并说明理由.

Answer 1

【答案】（1），；（2）2；（3）证明见解析；（4）相切

【解析】（1）将点A的坐标代入二次函数表达式中可求出a值，进而可得出二次函数表达式；

（2）将点B的坐标代入一次函数表达式中可求出b值；

（3）过点M作ME⊥y轴于点E，设点M的坐标为（x，x2+1），则MC=x2+1，由勾股定理可求出MB的长度，进而可证出MB=MC；

（4）过点N作ND⊥x轴于D，取MN的中点为P，过点P作PF⊥x轴于点F，过点N作NH⊥MC于点H，交PF于点Q，由（3）的结论可得出MN=NB+MB=ND+MC，利用中位线定理可得出PQ=MH，进而可得出PF=MN，由此即可得出以MN为直径的圆与x轴相切．

（1）∵二次函数y=ax2+1（a≠0，a为实数）的图象过点A（-2，2），

∴2=4a+1，解得：a=，

∴二次函数表达式为y=x2+1．

（2）∵一次函数y=kx+b（k≠0，k，b为实数）的图象l经过点B（0，2），

∴2=k×0+b，

∴b=2．

（3）证明：过点M作ME⊥y轴于点E，如图1所示．

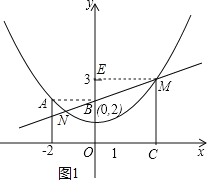
设点M的坐标为（x，x2+1），则MC=x2+1，

∴ME=|x|，EB=|x2+1-2|=|x2-1|，

∴MB= x2+1．

∴MB=MC．

（4）相切，理由如下：

过点N作ND⊥x轴于D，取MN的中点为P，过点P作PF⊥x轴于点F，过点N作NH⊥MC于点H，交PF于点Q，如图2所示．

由（3）知NB=ND，

∴MN=NB+MB=ND+MC．

∵点P为MN的中点，PQ∥MH，

∴PQ=MH．

∵ND∥HC，NH∥DC，且四个角均为直角，

∴四边形NDCH为矩形，

∴QF=ND，

∴PF=PQ+QF=MH+ND=（ND+MH+HC）=（ND+MC）=MN．

∴以MN为直径的圆与x轴相切．