��Ŀ����
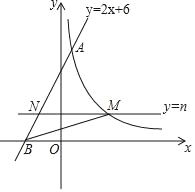
����Ŀ����ͼ��ֱ��y=2x+6�뷴��������y=![]() ��k��0����ͼ���ڵ�A��1��m������x�ύ�ڵ�B��ƽ����x���ֱ��y=n��0��n��6����������������ͼ���ڵ�M����AB�ڵ�N������BM��
��k��0����ͼ���ڵ�A��1��m������x�ύ�ڵ�B��ƽ����x���ֱ��y=n��0��n��6����������������ͼ���ڵ�M����AB�ڵ�N������BM��
��1����m��ֵ�ͷ����������ı���ʽ��
��2���۲�ͼ��ֱ��д����x��0ʱ����ʽ2x+6��![]() ��0�Ľ⼯��
��0�Ľ⼯��
��3��ֱ��y=n��y�᷽��ƽ�ƣ���nΪ��ֵʱ����BMN�����������ֵ�Ƕ��٣�
���𰸡���1�������������Ľ���ʽΪy=![]() ����2��0��x��1����3��
����2��0��x��1����3��![]() ��
��
����������������1���ѵ�A��1��m������ֱ��y=2x+6�����m��ֵ���ٰѵ�A���������y=![]() �����ô���ϵ�������ɽ�����⣻
�����ô���ϵ�������ɽ�����⣻
��2������ͼ��������ĺ���ֵ����ͼ������ĺ���ֵд���𰸼��ɣ�
��3���������κ��������ö��κ��������ʼ��ɽ�����⣻
��⣺��1����ֱ��y=2x+6������A��1��m����
��m=2��1+6=8��
��A��1��8����
�߷���������������A��1��8����
��k=8��
�෴���������Ľ���ʽΪy=![]() ��
��
��2������ʽ2x+6��![]() ��0�Ľ⼯Ϊ0��x��1��
��0�Ľ⼯Ϊ0��x��1��
��3�������⣬��M��N������ΪM��![]() ��n����N��
��n����N��![]() ��n����
��n����
��0��n��6��
��![]() ��0��
��0��
��![]() ��
��![]() ��0
��0
��S��BMN=![]() |MN|��|yM|=
|MN|��|yM|=![]() ����
����![]() ��
��![]() ����n=��
����n=��![]() ��n��3��2+
��n��3��2+![]() ��
��
��n=3ʱ����BMN�����������ֵΪ![]() ��
��

 ͬ��������ϰϵ�д�
ͬ��������ϰϵ�д� �ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�
�ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�����Ŀ�������ҹ����ʡ���������ظɺ����ܺ��ֵ�Ӱ�죬4�·ݣ�����ij�߲˼۸���������ƣ���ǰ����ÿ�ܵ�ƽ�����ۼ۸�仯�����
����x | 1 | 2 | 3 | 4 |
�۸�y��Ԫ/ǧ�ˣ� | 2 | 2.2 | 2.4 | 2.6 |
��1����۲����еı�������ѧ����һ�κ�������������������κ������й�֪ʶֱ��д��4�·�y��x�ĺ�����ϵʽ��
��2������5�£����ڱ����߲˵����У������߲˵�ƽ�����ۼ۸�y��Ԫ/ǧ�ˣ���5�µ�1�ܵ�2.8Ԫ/ǧ���½�����2�ܵ�2.4Ԫ/ǧ�ˣ���y������x�ı仯���������κ���y����![]() x2+bx+c�������5�·�y��x�ĺ�����ϵʽ��
x2+bx+c�������5�·�y��x�ĺ�����ϵʽ��
��3����4�·ݴ����߲˵Ľ���m��Ԫ/ǧ�ˣ�������x������ĺ�����ϵΪm��![]() x+1.2��5�·ݴ����߲˵Ľ���m��Ԫ/ǧ�ˣ�������x������ĺ�����ϵΪm����
x+1.2��5�·ݴ����߲˵Ľ���m��Ԫ/ǧ�ˣ�������x������ĺ�����ϵΪm����![]() x+2������4�·���5�·ݷֱ�����һ�����۴����߲�һǧ�˵�����������������ֱ��Ƕ��٣�
x+2������4�·���5�·ݷֱ�����һ�����۴����߲�һǧ�˵�����������������ֱ��Ƕ��٣�