题目内容
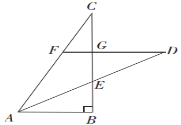
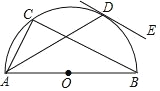
【题目】如图,点I是△ABC的内心,AI的延长线交边BC于点D,交△ABC的外接圆于点E.
(1)求证:IE=BE;
(2)若IE=4,AE=8,求DE的长.

【答案】(1)详见解析;(2)DE=2.
【解析】
(1)连接IB,只需证明∠IBE=∠BIE.根据三角形的外角的性质、三角形的内心是三角形的角平分线的交点以及圆周角定理的推论即可证明;
(2)IE的长,即是BE的长,则可以把要求的线段和已知的线段构造到两个相似三角形中,进行求解.
解: 连结IB.
∵点I是△ABC的内心,
∴∠BAD=∠CAD,∠ABI=∠IBD.
又∵∠BIE=∠BAD+∠ABI,
∴∠BIE=∠CAD+∠IBD=∠DBE+∠IBD=∠IBE,
∴BE=IE;
(2)在△BED和△AEB中,
∵∠EBD=∠CAD=∠EAB,∠BED=∠AEB,
∴△BED∽△AEB,
∴![]() =
=![]() .
.
∵IE=4,
∴BE=4.
∵AE=8,
∴DE=![]() =2.
=2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目