题目内容
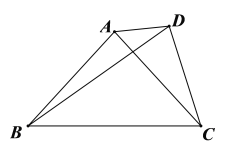
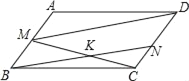
【题目】在ABCD中,AB=1,BC=2,∠B=45°,M为AB的中点.
(1)求tan∠CMD的值;
(2)设N为CD中点,CM交BN于K,求![]() 及S△BKC的值.
及S△BKC的值.
【答案】(1)tan∠CMD=![]() ;(2)
;(2)![]() ,
,![]() .
.
【解析】
(1)过点M作MF⊥BC于F,交DA的延长线于E,作DG⊥MC交MC的延长线
于G,①求出ME,MF,BF的长,②求出MC的长,③求出ABCD的面积,△MCD的面
积,④由△MCD的面积,求出DG的长,⑤由勾股定理求出CG的长,⑥求出MG的长,
⑦在Rt△MDG中,求出tan∠CMD的值.
(2)易证明△KBM≌△KNC,∴BK=BN,∴![]()
![]()
解:(1)过点M作MF⊥BC于F,交DA的延长线于E,作DG⊥MC交MC的延长线于G,
∵在ABCD中,AB=1,BC=2,∠B=45°,M为AB的中点.
∴BM=AM=![]() ,∠EAM=∠B=45°,
,∠EAM=∠B=45°,
∴△AEM、△BFM是等腰直角三角形,
∴AE=EM=BF=MF=![]()
∴![]()
∴![]()
∵AE=EM=BF=MF=![]()
∴EF=EM+FM=![]()
∴SABCD=ADEF=![]() ,
,
∵点M是AB的中点,
∴![]()
∵![]()
∴![]()
在Rt△CDG中,由勾股定理得:
![]()
∴
![]()
在Rt△MDG中,
tan∠CMD=![]()

(2)在ABCD中,M为AB的中点,N为CD中点,
∴BM=CN,
∵AB∥CD,
∴∠MBK=∠CNK,∠BMK=NCK,
在△BMK和△NCK中,

∴△BMK≌△NCK(ASA)
∴BK=NK,MK=CK,
∴![]()
∵MK=CK,
∴![]()

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目