Question

【题目】在平面直角坐标系中，直线y＝x+b与x轴交于点A，与y轴交于点B，点P坐标为（3，0），过点P作PC⊥x轴于P，且△ABC为等腰直角三角形．

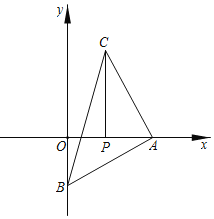
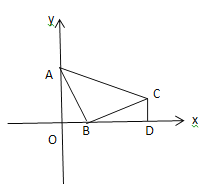
（1）如图，当∠BAC＝90°，AB＝AC时，求证△ABO≌△CAP；

（2）当AB为直角边时，请直接写出所有可能的b值．

Answer 1

【答案】（1）证明见解析；（2）当AB为直角边时，所有可能的b值为﹣3或3或﹣1．

【解析】

(1)通过题意可得∠CPA=∠AOB=90°,AB=CA,再根据互余的性质求出∠OAB=∠PCA,即可证明.

(2)将直线在坐标轴上平移即可分三类情况讨论.

(1)证明：∵∠BAC＝90°,

∴∠OAB+∠CAP＝90°,

∵PC⊥x轴,

∴∠CPA＝90°,

∴∠PCA+∠CAP＝90°,

∴∠OAB＝∠PCA,

∵∠AOB＝90°,

∴∠AOB＝∠CPA,

在△ABO和△CAP中,,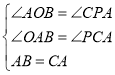

∴△ABO≌△CAP(AAS)；

(2)解：分三种情况：

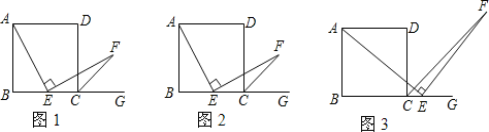
①如图1所示：

∵直线y＝x+b与x轴交于点A,与y轴交于点B,

∴A(﹣2b,0),B(0,b),

∴OA＝﹣2b,OB＝﹣b,

∵点P坐标为(3,0),

∴OP＝3,

由(1)得：△ABO≌△CAP(AAS),

∴OB＝AP＝﹣b,

∴OP＝OA﹣AP＝﹣b＝3,

∴b＝﹣3；

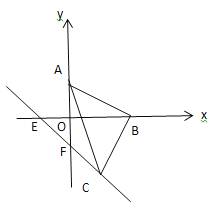
②如图2所示：

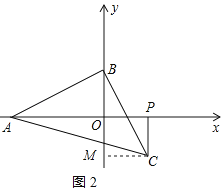
作CM⊥y轴于M,则CM＝OP＝3,

同①得：△ABO≌△BCM(AAS),

∴OB＝CM＝3,

∴b＝3；

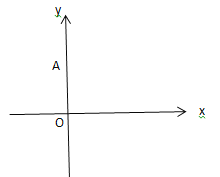
③如图3所示：

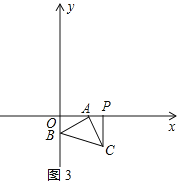
同①得：△ABO≌△CAP(AAS),

∴OB＝AP＝﹣b,

∵OA＝﹣2b,OA+AP＝3,

∴﹣2b﹣b＝3,

∴b＝﹣1；

综上所述,当AB为直角边时,所有可能的b值为﹣3或3或﹣1．