题目内容
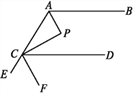
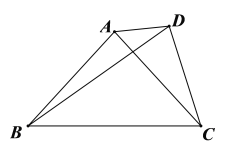
【题目】如图，在
中，
，点
和点
在直线
的同侧，
，连接
，则
的度数为__________．
【答案】30°
【解析】
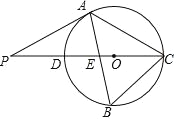
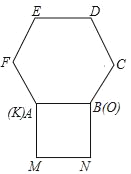
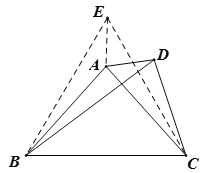
先根据等腰三角形的性质和三角形的内角和定理以及角的和差求出
的度数，然后作点D关于直线AB的对称点E，连接BE、CE、AE，如图，则BE=BD，∠EBA=∠DB，∠BEA=∠BDA，进而可得∠EBC=60°，由于BD=BC，从而可证△EBC是等边三角形，可得∠BEC=60°，EB=EC，进一步即可根据SSS证明△AEB≌△AEC，可得∠BEA的度数，问题即得解决．
解：∵
，
，∴
，
∵
，∴
，
作点D关于直线AB的对称点E，连接BE、CE、AE，如图，则BE=BD，∠EBA=∠DBA=11°，∠BEA=∠BDA，
∴∠EBC=11°+11°+38°=60°，
∵BD=BC，∴BE=BC，∴△EBC是等边三角形，∴∠BEC=60°，EB=EC，
又∵AB=AC，EA=EA，
∴△AEB≌△AEC（SSS），∴∠BEA=∠CEA=
，
∴∠ADB=30°．
练习册系列答案
相关题目
【题目】某中学决定在“五·四艺术周”为一个节目制作A、B两种道具，共80个． 制作的道具需要甲、乙两种材料组合而成，现有甲种材料700件，乙种材料500件，已知组装A、B两种道具所需的甲、乙两种材料，如下表所示：
甲种材料（件） | 乙种材料（件） | |
A道具 | 6 | 8 |
B道具 | 10 | 4 |
经过计算，制作一个A道具的费用为5元，一个B道具的费用为4.5元． 设组装A种道具x个，所需总费用为y元．
（1）求y与x的函数关系式，并求出x的取值范围；
（2）问组装A种道具多少个时，所需总费用最少，最少费用是多少？
