题目内容
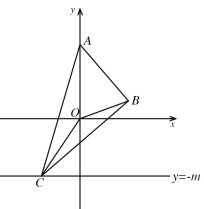
【题目】已知:如图,在平面直角坐标系中,![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,过点
,过点![]() 画
画![]() 交直线
交直线![]() 于
于![]() (即点
(即点![]() 的纵坐标始终为
的纵坐标始终为![]() ),连接
),连接![]() .
.
(1)求![]() 的长.
的长.
(2)若![]() 为等腰直角三角形,求
为等腰直角三角形,求![]() 的值.
的值.
(3)在(2)的条件下求![]() 所在直线的表达式.
所在直线的表达式.
(4)用![]() 的代数式表示
的代数式表示![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]()
【解析】
(1)用两点间的距离公式即可求出AB的长;
(2)过B作直线l∥y轴,与直线![]() 交于点E,过A作AD⊥l于点D,证明△ABD≌△BCE,得到
交于点E,过A作AD⊥l于点D,证明△ABD≌△BCE,得到![]() ,
,![]() ,从而推出C点坐标,即可得到m的值;
,从而推出C点坐标,即可得到m的值;
(3)设BC直线解析式为![]() ,代入B,C坐标求出k,b,即可得解析式;
,代入B,C坐标求出k,b,即可得解析式;
(4)根据(3)中的解析式求得直线BC与y轴的交点F的坐标,将△BOC分成△COF和△BOF计算即可.
(1)∵![]() ,
,![]()
∴![]()
(2)如图,过B作直线l∥y轴,与直线![]() 交于点E,过A作AD⊥l于点D,
交于点E,过A作AD⊥l于点D,

可得∠ADB=∠BEC=90°,D(3,5)
∴∠BAD+∠ABD=90°
∵![]() 是等腰直角三角形
是等腰直角三角形
∴AB=BC,∠ABC=90°
∴∠CBE+∠ABD=90°
∴∠BAD=∠CBE
在△ABD和△BCE中,
∵∠ADB=∠BEC,∠BAD=∠CBE,AB=BC
∴△ABD≌△BCE(AAS)
∴DB=CE=5-1=4,BE=AD=3
∴C点横坐标为![]() ,纵坐标为
,纵坐标为![]()
即![]() ,
,
∴![]()
(3)设BC直线解析式为![]() ,
,
∵直线过![]() ,
,![]()
∴![]() ,解得
,解得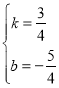
∴![]()
(4)∵m变化时,BC直线不会发生变化,
则![]() ,
,
设直线BC与y轴交于点F,直线![]() 与y轴交于点H,
与y轴交于点H,
当![]() 时,
时,![]() ,
,
∴F![]()
当y=-m时,![]() ,解得
,解得![]()
∴C![]()
∴S△BOC=S△COF+S△BOF
=![]()
=![]()
=![]()
=![]()
=![]()

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目