题目内容
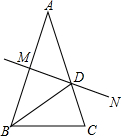 如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于点M,有下面3个结论:
如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于点M,有下面3个结论:
①射线BD是∠ABC的角平分线;②△BCD是等腰三角形;③△AMD≌△BCD.
(1)判断其中正确的结论是哪几个?
(2)从你认为是正确的结论中选一个加以证明.
解:(1)正确的结论是①、②;
(2)若①正确,理由如下:
∵MN是AB的中垂线,
∴DA=DB,
则∠A=∠ABD=36°,
又等腰三角形ABC中,AB=AC,∠A=36°,
∴∠C=∠ABC=72°,∴∠DBC=36°,
则BD是∠ABC的平分线;
若②正确,理由如下:
由①知:∠C=72°,∠DBC=36°,
∴∠BDC=72°,即∠C=∠BDC,
∴BD=BC,即△BCD是等腰三角形.
分析:(1)正确的结论是①和②;
(2)若选择①,根据MN为线段AB的中垂线,利用线段垂直平分线定理得到DA=DB,再根据等边对等角可得∠A=∠ABD,由等腰三角形ABC及顶角的度数求出底角的度数,利用∠DBC=∠ABC-∠ABD求出∠DBC的度数,进而得到∠ABD=∠DBC,即BD为角平分线;
若选择②,由①求出的∠C和∠DBC的度数,求出∠BDC的度数,发现∠C=∠BDC,根据等角对等边可得BD=BC,即三角形BCD为等腰三角形.
点评:此题考查了线段垂直平分线定理,等腰三角形的判定与性质,三角形的内角和定理,以及三角形的外角性质,要求学生借助图形,熟练运用定理及性质,利用转化的思想达到解决问题的目的.
(2)若①正确,理由如下:
∵MN是AB的中垂线,
∴DA=DB,
则∠A=∠ABD=36°,
又等腰三角形ABC中,AB=AC,∠A=36°,
∴∠C=∠ABC=72°,∴∠DBC=36°,
则BD是∠ABC的平分线;
若②正确,理由如下:
由①知:∠C=72°,∠DBC=36°,
∴∠BDC=72°,即∠C=∠BDC,
∴BD=BC,即△BCD是等腰三角形.
分析:(1)正确的结论是①和②;
(2)若选择①,根据MN为线段AB的中垂线,利用线段垂直平分线定理得到DA=DB,再根据等边对等角可得∠A=∠ABD,由等腰三角形ABC及顶角的度数求出底角的度数,利用∠DBC=∠ABC-∠ABD求出∠DBC的度数,进而得到∠ABD=∠DBC,即BD为角平分线;
若选择②,由①求出的∠C和∠DBC的度数,求出∠BDC的度数,发现∠C=∠BDC,根据等角对等边可得BD=BC,即三角形BCD为等腰三角形.
点评:此题考查了线段垂直平分线定理,等腰三角形的判定与性质,三角形的内角和定理,以及三角形的外角性质,要求学生借助图形,熟练运用定理及性质,利用转化的思想达到解决问题的目的.

练习册系列答案
相关题目
 如图,已知AB⊥AC,AD⊥AE,AB=AC,AD=AE,则∠BFD的度数是( )
如图,已知AB⊥AC,AD⊥AE,AB=AC,AD=AE,则∠BFD的度数是( )| A、60° | B、90° | C、45° | D、120° |
 10、如图,已知AB=AC,D是BC的中点,E是AD上的一点,图中全等三角形有几对( )
10、如图,已知AB=AC,D是BC的中点,E是AD上的一点,图中全等三角形有几对( ) 26、如图,已知AB=AC,AD=AE.求证BD=CE.
26、如图,已知AB=AC,AD=AE.求证BD=CE. 2、如图,已知AB=AC,AD=AE,BD=EC,则图中有
2、如图,已知AB=AC,AD=AE,BD=EC,则图中有 如图,已知AB=AC,BC=CD=AD,求∠B的值.
如图,已知AB=AC,BC=CD=AD,求∠B的值.