题目内容
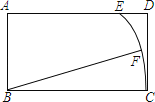
【题目】如图,在矩形ABCD中,AB=3,BC=5,以B为圆心BC为半径画弧交AD于点E,如果点F是弧EC的中点,联结FB,那么tan∠FBC的值为 .
考点:全等三角形的判定与性质;角平分线的性质;矩形的性质;圆心角、弧、弦的关系;解直角三角形.
【答案】
【解析】
试题分析:连接CE交BF于H,连接BE,根据矩形的性质求出AB=CD=3,AD=BC=5=BE,∠A=∠D=90°,根据勾股定理求出AE=4,求出DE=1,根据勾股定理求出CE,求出CH,解直角三角形求出即可.
解:连接CE交BF于H,连接BE,
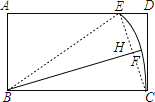
∵四边形ABCD是矩形,AB=3,BC=5,
∴AB=CD=3,AD=BC=5=BE,∠A=∠D=90°,
由勾股定理得:AE=![]() =4,DE=5﹣4=1,
=4,DE=5﹣4=1,
由勾股定理得:CE=![]() =
=![]() ,
,
由垂径定理得:CH=EH=![]() CE=
CE=![]() ,
,
在Rt△BFC中,由勾股定理得:BH=![]() =
=![]() ,
,
所以tan∠FBC=![]() =
=![]() =
=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目

