题目内容
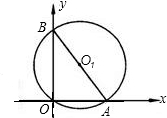
已知等腰△ABC中，AB=AC=13cm，BC=10cm，则△ABC的内切圆半径为______cm．
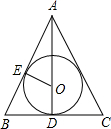
如图，∵AB=AC=13cm，BC=10cm，
∴BD=5cm，
∴AD=12cm，
根据切线长定理，AE=AB-BE=AB-BD=13-5=8，
设△ABC的内切圆半径为r，
∴AO=12-r，
∴（12-r）2-r2=64，
解得r=
，
故答案为
．
∴BD=5cm，
∴AD=12cm，
根据切线长定理，AE=AB-BE=AB-BD=13-5=8，
设△ABC的内切圆半径为r，
∴AO=12-r，
∴（12-r）2-r2=64，
解得r=
| 10 |
| 3 |
故答案为
| 10 |
| 3 |
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
