题目内容
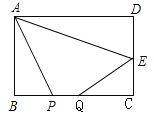
【题目】如图,在矩形ABCD中 ,AB=4,BC=8,点E为CD中点,P、Q为BC边上两个动点,且PQ=2,当四边形APQE周长最小时,BP的长为( )
A. 1 B. 2 C. 2![]() D. 4
D. 4
【答案】D
【解析】要使四边形APQE的周长最小,由于AE与PQ都是定值,只需AP+EQ的值最小即可.为此,先在BC边上确定点P、Q的位置,可在AD上截取线段AF=DE=2,作F点关于BC的对称点G,连接EG与BC交于一点即为Q点,过A点作FQ的平行线交BC于一点,即为P点,则此时AP+EQ=EG最小,然后过G点作BC的平行线交DC的延长线于H点,那么先证明∠GEH=45°,再由CQ=EC即可求出BP的长度.
如图,在AD上截取线段AF=DE=2,作F点关于BC的对称点G,连接EG与BC交于一点即为Q点,过A点作FQ的平行线交BC于一点,即为P点,过G点作BC的平行线交DC的延长线于H点.
∵GH=DF=6,EH=2+4=6,∠H=90°,
∴∠GEH=45°.
设BP=x,则CQ=BC-BP-PQ=8-x-2=6-x,
在△CQE中,
∵∠QCE=90°,∠CEQ=45°,
∴CQ=EC,
∴6-x=2,
解得x=4.
故选D.


练习册系列答案
相关题目