Question

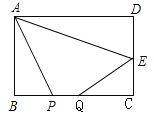
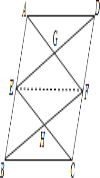
【题目】在□ABCD中，E、F分别是AB、CD的中点，AF与DE相交于点G，CE与BF相交于点H．

（1）求证：四边形EHFG是平行四边形；

（2）□ABCD应满足什么条件时，四边形EHFG是矩形？并说明理由；

（3）□ABCD应满足什么条件时，四边形EHFG是正方形？（不要说明理由）.

Answer 1

【答案】（1）（2）见解析；（3）AB=2AD且∠BAD=90°.

【解析】（1）通过证明两组对边分别平行，可得四边形EHFG是平行四边形；

（2）当AB=2AD时，先证明四边形ADFE是菱形，得出AF⊥DE，∠EGF＝90°，从而证明平行四边形EHFG为一个矩形；

（3）由（2）可知只要GE=GF时矩形EHFG是正方形，则可知需要AF=DE，即需要证明菱形ADEF是正方形，由此可知需要∠EAD=90°，据此即可确定□ABCD应满足的条件.

（1）∵四边形ABCD是平行四边形，

∴AE∥CF，AB=CD，

∵E是AB中点，F是CD中点，

∴AE=CF，

∴四边形AECF是平行四边形，

∴AF∥CE．

同理可得DE∥BF，

∴四边形FGEH是平行四边形；

（2）AB=2AD，理由如下：连接EF，

∵E，F分别为AB，CD的中点，且AB＝CD，

∴AE＝DF，且AE∥DF，

∴四边形AEFD为平行四边形，

∴AD＝EF，

又∵AB＝2AD，E为AB中点，则AB＝2AE，

∴AE＝AD，

∴四边形AEFD为菱形，

∴AF⊥DE，∠EGF＝90°，

∴平行四边形EHFG是矩形；

（3）AB=2AD且∠BAD=90°，理由如下：

由（2）可知当AB=2AD时，四边形EHFG是矩形，四边形AEFD是菱形，

∵∠BAD=90°，∴菱形AEFD是正方形，

∴AF=DE，ED=2EG，AF=2GF，

∴GE=GF，

∴矩形EHFG是正方形.