Question

【题目】)矩形中，.分别以所在直线为轴，轴，建立如图1所示的平面直角坐标系.是边上一个动点(不与重合)，过点的反比例函数y=()的图像与边交于点.

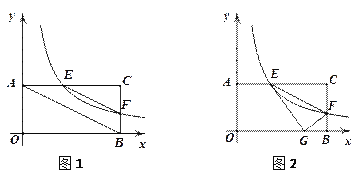
(1)当点运动到边的中点时，求点的坐标；

(2)连接EF、AB，求证：EF∥AB；

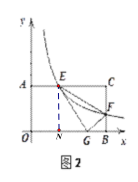
(3)如图2，将沿折叠，点恰好落在边上的点处，求此时反比例函数的解析式.

Answer 1

【答案】(1)E(4，4) ；(2)见解析；(3)

【解析】(1)先求F坐标，再求函数解析式，再求E坐标；

（2）由平行线分线段成比例性质定理可得.即由 ，，得,故得EF∥AB；

（3）过点E作EN⊥OB,垂足为N，先证△ENG∽△GBF,得 即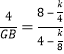，可求GB=2，由GB2+BF2=GF2，得，解得，k=12，故.

因为F是BC的中点，

所以，BF=2，

所以，F（8，2）

把F（8，2）代入y=，得2=，

解得k=16,

所以，y=

当y=4时，x=4

所以，E（4，4）

（2）由已知可设E（，4），F（8，）

所以，EC=8-,CF=4-.

所以， ，

所以，,

所以，EF∥AB；

（3）过点E作EN⊥OB,垂足为N

由题意得，EN=AO=4,EG=EC=8- ，GF=CF=4-，

因为，∠EGN+∠FGB=∠FGB+∠GFB=900

所以，∠EGN=∠GFB，

又因为，∠ENG=∠GBF=900

所以，△ENG∽△GBF,

所以，

所以， ，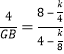

整理得，GB=2，

因为，GB2+BF2=GF2

所以， ，

解得，k=12

所以，.