题目内容
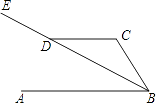
【题目】如图,四边形ABCD中,∠A=∠C=90°,BE、DF分别平分∠ABC、∠ADC,判断BE、DF是否平行,并说明理由.
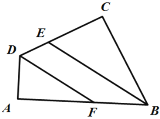
【答案】BE∥DF,理由见解析.
【解析】
根据四边形的内角和为360°得到∠ADC+∠ABC=180°,再根据角平分线的性质得到∠ABE+∠ADF =90°,再由等量替换得到∠AFD=∠ABE,根据同位角相等两直线平行即可得到;
BE∥DF,理由如下:
证明:四边形ABCD中,∠A=∠C=90°,
∴∠ADC+∠ABC=180°,
∵BE平分∠ABC,DF平分∠ADC,
∴∠ADF=∠FDC,∠ABE=∠CBE,
∴∠ABE+∠ADF =90°,
∵∠AFD+∠ADF=90°,
∴∠AFD=∠ABE(等量替换),
∴BE∥DF(同位角相等,两直线平行).

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目