题目内容
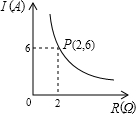
如图,已知双曲线y=
(k>0)经过直角三角形OAB斜边OB的中点D,与直角边AB相交于点C,DE⊥x轴于点E.若△OBC的面积为6,则k=______.

| k |
| x |

过D点作DE⊥x轴,垂足为E,
由双曲线上点的性质,得S△AOC=S△DOE=
k,
∵DE⊥x轴,AB⊥x轴,
∴DE∥AB,
∴△OAB∽△OED,
又∵OB=2OD,
∴S△OAB=4S△DOE=2k,
由S△OAB-S△OAC=S△OBC,
得2k-
k=6,
解得k=4.
故答案为:4.
由双曲线上点的性质,得S△AOC=S△DOE=
| 1 |
| 2 |
∵DE⊥x轴,AB⊥x轴,
∴DE∥AB,
∴△OAB∽△OED,
又∵OB=2OD,
∴S△OAB=4S△DOE=2k,
由S△OAB-S△OAC=S△OBC,
得2k-
| 1 |
| 2 |
解得k=4.
故答案为:4.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 过点C作CD⊥y轴,垂足为D,且△BCD的面积为1.
过点C作CD⊥y轴,垂足为D,且△BCD的面积为1.
 D两点.
D两点.